集合初步
概念
一切都可成为研究对象.
集合: 研究对象所汇总成的集体.
元素: 构成集合的每个研究对象.
元素(不)属于集合,用$\in$表示属于,用$\notin$表示不属于.
集合的三大特性
- 确定性: 集合的元素必须是确定的.
- 无序性: 集合中的元素可以任意排列.
- 互异性: 对于给定的一个集合,集合中的元素必须是不同的.
例1 已知$\{a, \dfrac{b}{a}, 1\} = \{a^2, a + b, 0\}$,则$a^{2022} + b^{2023} = \underline{\qquad\qquad}$.
观察得,$a$或$\dfrac{b}{a}$为$0$,但$a^2 \neq 0$,所以$b = 0$.
则有$\{a, 0, 1\} = \{a^2, a, 0\}$.
所以$a^2 = 1$,则$a = \pm 1$.
又因为$a \neq 1$,所以$a = -1$.
则$a^{2022} + b^{2023} = (-1)^{2022} + 0^{2023} = 1$.
注意: 如果$S = \{a, 2, 3\}$,则$a \notin \{2, 3\}$;集合内部有参数,小心“互异性”!
集合的表示方法
常见数集:
$\mathbb{N}$: 自然数集.
$\mathbb{N_+}$: 正整数集.
$\mathbb{Z}$: 整数集.
$\mathbb{Q}$: 有理数集.
$\mathbb{R}$: 实数集.
示例1: 表示出“大于$1$小于$5$的整数”构成的集合.
1.列举法: $\{2, 3, 4\}$.
2.描述法: $\{x \in \mathbb{Z} \,|\, 1 < x < 5\}$.
示例2: 表示出下列集合.
1.绝对值小于$3$的整数构成的集合.
列举法: $\{0, \pm 1, \pm 2\}$.
描述法: $\{x \in \mathbb{Z} \,|\, \lvert x \rvert < 3\}$.
2.所有偶数构成的集合.
列举法: $\{0, \pm 2, \pm 4, \pm 6, \cdots\}$.
描述法: $\{x \,|\, x = 2k,\; k \in \mathbb{Z}\}$
3.第一象限的点所构成的集合.
$\{(x, y) \,|\, x > 0,\; y > 0\}$.
例2 设$A = \{4, 5, 6\}$,$B = \{1, 2, 3\}$,求集合$C = \{x \,|\, x = m - n,\; m \in A ,\; n \in B\}$中的所有元素之和.
$x$的最小值: $x_{min} = m_{min} - n_{max} = 4 - 3 = 1$.
$x$的最大值: $x_{max} = m_{max} - n_{min} = 6 - 1 = 5$.
据题意,$m \in \mathbb{Z}$,$n \in \mathbb{Z}$.
所以$x \in \mathbb{Z}$.
所以$C = \{1, 2, 3, 4, 5\}$.
所有元素之和$1 + 2 + 3 + 4 + 5 = 15$.
集合间关系
空集
空集是一个没有元素的集合,用$\varnothing$表示.
例1 已知集合$M = \{x \,|\, 2m < x < m + 1\}$,且$M = \varnothing$,则实数$m$的取值范围是$\underline{\qquad\qquad}$.
因为$M = \varnothing$.
所以$2m \geq m + 1$.
解得$m \geq 1$.
则实数$m$的取值范围是$\{m \,|\, m \geq 1\}$. (注意写成集合形式)
注意: 如果$S = \{x \,|\, 2a + 3 < x < a - 2\}$,注意$2a + 3 \geq a - 2$的情况;集合里有参数,注意空集!
子集
如果集合$A$中任意一个元素都属于集合$B$,则称集合$A$是集合$B$的子集,记作$A \subseteq B$.
情况一: 真子集
记作$A \subsetneqq B$.
即$A \subseteq B$且$A \neq B$.
情况二: 两集合相等
记作$A = B$,即$A \subseteq$ B且$B \subseteq A$.
情况三: 空集
当$A = \varnothing$时,$A \subseteq B$.
规定: 空集是任意非空集合的子集.
对于有$n$个元素的非空集合$A$,其中$n > 1$:
子集个数: $2^n$.
真子集个数: $2^n - 1$.
非空子集个数: $2^n - 1$.
非空真子集个数: $2^n - 2$.
例2 已知集合$A = \{x \,|\, -2 < x \leq 5\}$,$B = \{x \,|\, m + 1 \leq x \leq 2m - 1\}$,若$B \subseteq A$,则实数$m$的取值范围是$\underline{\qquad\qquad}$.
$1)$ 当$B \neq \varnothing$时,
画图
得$-2 < m + 1 \leq 2m - 1 \leq 5$.
解得$\left\{\begin{array}{lr}m > -3 \\ m \geq 2 \\ m \leq 3\end{array}\right.$
所以$2 \leq m \leq 3$.
$2)$ 当$B = \varnothing$时,
此时$2m - 1 > m + 1$,解得$m < 2$.
综上所述,$m$的取值范围是$\{m \,|\, m \leq 3\}$.
例3 集合$A = \{x \,|\, x < -1 或 x \geq 3\}$,$B = \{x \,|\, ax + 1 \leq 0\}$,若$B \subseteq A$,求实数$a$的取值范围.
据题意$ax \leq -1$.
$1)$ 当$a = 0$时,
得$0 \leq -1 \implies B = \varnothing$
此时有$B \subseteq A$.
$2)$ 当$a > 0$时,
得$x \leq -\dfrac{1}{a}$.
画图
得$-\dfrac{1}{a} < -1$.
所以$a < 1$
则当$0 < a < 1$时,有$B \subseteq A$.
$3)$ 当$a < 0$时,
画图
得$-\dfrac{1}{a} \geq 3$.
解得$a \geq -\dfrac{1}{3}$.
则当$-\dfrac{1}{3} \leq a < 0$时,有$B \subseteq A$.
综上所述,实数$a$的取值范围是$\{a \,|\, -\dfrac{1}{3} \leq a < 1\}$.
例4 集合$A = \{x \,|\, -1 < x < 3,\; x \in \mathbb{N}\}$的子集的个数是$\underline{\qquad\qquad}$个;集合$B = \{1, 2, 3, 4, 5, 6\}$的子集的个数是$\underline{\qquad\qquad}$个.
如果集合有$n$个元素,那么它的子集个数有$2^n$个.
故集合$A$有$2^3 = 8$个子集,集合$B$有$2^6$个子集.
集合的运算
- 交集
记作$A \cap B$.
即$A$且$B$. - 并集
记作$A \cup B$.
即$A$或$B$. - 补集
在全集$U$中,除集合$A$以外的部分叫做集合$A$的补集,记作$\complement_UA$.
一般地,全集$U$为Venn图中的矩形.
典例1 已知集合$U = \{-2, -1, 0, 1, 2\}$,$A = \{0, 1\}$,$B = \{-1, 0, 1\}$,则
$1)$ $A \cap B = \{0, 1\}$.
$2)$ $A \cup B = \{-1, 0, 1\}$.
$3)$ $\complement_UA = \{-2, -1, 2\}$.
$4)$ $\complement_BA = \{-1\}$.
典例2 设全集$U = \mathbb{R}$,集合$A = \{x \,|\, x \geq 1\}$,$B = \{x \,|\, x < 2\}$,则
$1)$ $A \cup B = \mathbb{R}$.
$2)$ $A \cap B = \{x \,|\, 1 \leq x < 2\}$.
$3)$ $\complement_UA = \{x \,|\, x < 1\}$.
$4)$ $\complement_U(A \cap B) = \{x \,|\, x < 1 \, 或 \, x \geq 2\}$.
例1 已知集合$A = \{x \,|\, 3 \leq x \leq 6\}$,$\complement_\mathbb{R}B = \{x \,|\, 2 \leq x \leq 5\}$,求$A \cup B$,$(\complement_\mathbb{R}A) \cap B$.
因为$\complement_\mathbb{R}B = \{x \,|\, 2 \leq x \leq 5\}$,
所以$B = \{x \,|\, x < 2 \,或\, x > 5\}$.
则$A \cup B = \{x \,|\, x < 2 \,或\, x \geq 3\}$.
因为$A = \{x \,|\, 3 \leq x \leq 6\}$,
所以$\complement_\mathbb{R}A = \{x \,|\, x < 3 \,或\, x > 6\}$.
则$(\complement_\mathbb{R}A) \cap B = \{x \,|\, x < 2 \,或\, x > 6\}$.
例2 学校先举办了一次田径运动会,某班有$8$名同学参赛,又举办了一次球类运动会,该班有$12$名同学参赛,两次运动会都参赛的有$3$人.两次运动会中,该班参赛的同学总共有$\underline{\qquad\qquad}$人.
画出Venn图
得该班参赛的同学共有$5 + 3 + 9 = 17$人.
例3 已知全集为$U$,集合$A$,$B$如图所示,则图中的阴影部分表示的集合为$(\qquad)$.
$\mathrm{A}. (\complement_UA) \cap B \qquad\qquad \mathrm{B}. \complement_U(A \cap B) \qquad\qquad \mathrm{C}. \complement_B(A \cap B) \qquad\qquad \mathrm{D}. A \cap (\complement_UB)$
分别画出Venn图.
$\mathrm{A}.$
$\mathrm{B}.$
$\mathrm{C}.$
$\mathrm{D}.$
故选择$\mathrm{AC}$.
例4 若集合$A$,$B$,$U$满足$A \cap (\complement_UB) = \varnothing$,则$(\qquad)$.
$\mathrm{A}. A \cap B = A \qquad\qquad \mathrm{B}. A \cup B = U \qquad\qquad \mathrm{C}. A \cup (\complement_UB) = U \qquad\qquad \mathrm{D}. B \cup (\complement_UA) = U$
画出$A \cap (\complement_UB) = \varnothing$,阴影部分为$\complement_UB$.
同上题过程,选择$\mathrm{AD}$.
综合大题例题
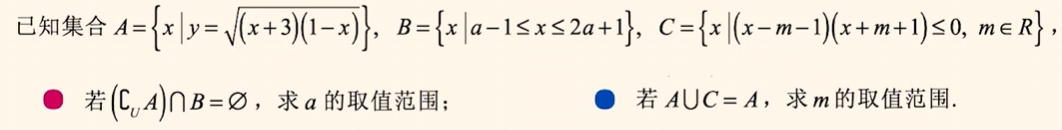
1)
画出$(\complement_UA) \cap B = \varnothing$.
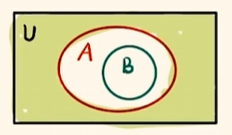
得$B \subseteq A$.
据题意 $A: (x + 3)(1 - x) \geq 0 \implies x \in [-3, 1]$.
- 当$B \neq \varnothing$时:
$-3 \leq a - 1 \leq 2a + 1 \leq 1 \implies a \in [-2, 0]$. - 当$B = \varnothing$时:
$2a + 1 < a - 1 \implies a \in (-\infty, -2)$.
综上,$a \in (-\infty, 0]$.
2)
画出$A \cup C = A$,得$C \subseteq A$.
据题意$C: x \in [m + 1, -m - 1]$或$x \in [-m - 1, m + 1]$.
$
\left\{
\begin{array}{lr}
-3 \leq m + 1 \leq 1 \\
-3 \leq -m - 1 \leq 1
\end{array}
\right.
$
解不等式得
$
\left\{
\begin{array}{lr}
-4 \leq m \leq 0 \\
-2 \leq m \leq 2
\end{array}
\right.
$
综上,$m \in [-2, 0]$.
逻辑用语
充分条件与必要条件
充分性推导: 由条件推出结论.
必要性推导: 由结论推出条件.
即在条件$P$,结论$Q$中:
充分不必要条件: $P \implies Q$,$P \subsetneqq Q$.
必要不充分条件: $Q \implies P$,$Q \subsetneqq P$.
充分必要(充要)条件: $P \iff Q$,$P = Q$.
小范围可以推大范围,大范围不可以推小范围.
全称量词与存在量词
全称量词: $\forall$.
存在量词: $\exists$.
对于命题$p$: $\forall x \in M$,$p(x)$,否定命题为$\lnot p$: $\exists x \in M$,$\lnot p(x)$.
对于命题$p$: $\exists x \in M$,$p(x)$,否定命题为$\lnot p$: $\forall x \in M$,$\lnot p(x)$.
对于命题$p$: $\forall x \in A$,$\exists y \in B$,$p(x)$,否定命题为$\lnot p$: $\exists x \in A$,$\forall y \in B$,$\lnot p(x)$.
对于命题$p$: $\forall x \in M$,$p_1(x)$或$p_2(x)$,否定命题为$\lnot p$: $\exists x \in M$,$\lnot p_1(x)$且$\lnot p_2(x)$.
示例:

据题意,真命题为$\forall x_0 \in \mathbb{R}$,$mx_0^2 + 2mx_0 -2 < 0$.
分情况讨论.
- 当$m > 0$时:
此时抛物线开口向上,一定有$mx_0^2 + 2mx_0 -2 > 0$,命题不成立. - 当$m = 0$时:
$-2 < 0$,命题成立. - 当$m < 0$时:
此时当抛物线与$y$轴无交点时,有$mx_0^2 + 2mx_0 -2 < 0$.
则$\Delta = 4m^2 + 8m < 0$,解得$m \in (-2, 0)$.
综上,$m$的取值范围是$(-2, 0]$.





