高中数学

概念

向量: 既有大小，又有方向的量.
相反向量: 大小相等，方向相反的向量.
单位向量: 模长为 $1$ 的向量，单位向量有无数多个.

表示法

  1. 一般向量
    • $\overrightarrow{AB}$
    • $\vec{a}$
    • $\boldsymbol{a}$
  2. 模长（大小）:
    • $| \overrightarrow{AB} |$
  3. 零向量（任意方向）:
    • $\vec{0}$
    • $\boldsymbol{0}$

向量的方向

  1. 垂直向量:
    $\boldsymbol{a} \perp \boldsymbol{b}$
  2. 平行向量（即共线向量）:
    $\boldsymbol{a} \parallel \boldsymbol{b} \parallel \boldsymbol{c}$
    其中 $\boldsymbol{a}$ 与 $\boldsymbol{b}$ 共线，与 $\boldsymbol{c}$ 反向.（共线 $\iff$ 平行）
  3. 既不平行，也不垂直.
  4. 规定: 零向量平行于任意一向量.

辨析

  1. 两个向量相等 $\iff$ 大小、方向均相同
  2. 向量可以随意平移.（性质）
  3. 平面向量 $\neq$ 有向线段.（有向线段不可平移）
  4. $\boldsymbol{a} = \boldsymbol{b}$ 与 $|\boldsymbol{a}| = |\boldsymbol{b}|$ 不同.
  5. 如果 $\boldsymbol{a} \parallel \boldsymbol{b}$，$\boldsymbol{b} \parallel \boldsymbol{c}$，则不一定有 $\boldsymbol{a} \parallel \boldsymbol{c}$，因为 $\boldsymbol{b}$ 有可能为 $\boldsymbol{0}$.

向量加法

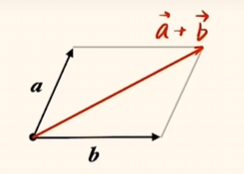
平行四边形法则

三角形法则

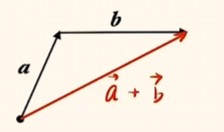
示例:

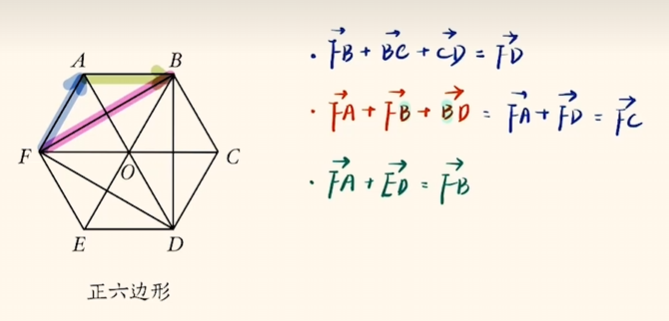
向量减法

对于$\overrightarrow{AB}$的相反向量$-\overrightarrow{AB}$，有$-\overrightarrow{AB} = \overrightarrow{BA}$.
则$\overrightarrow{OA} - \overrightarrow{OB} = \overrightarrow{OA} + \overrightarrow{BO} = \overrightarrow{BA}$.
示例:
如图，求$\overrightarrow{OA} - \overrightarrow{ED}$.

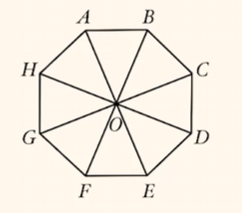
解 $\overrightarrow{OA} - \overrightarrow{ED} = \overrightarrow{OA} - \overrightarrow{HA} = \overrightarrow{OA} + \overrightarrow{AH} = \overrightarrow{OH}$.（或$\overrightarrow{DO}$）

向量数乘

在 $\lambda\boldsymbol{a}$中，$|\lambda\boldsymbol{a}| = \lambda|\boldsymbol{a}|$.
当 $\lambda > 0$ 时，方向不变，当 $\lambda = 0$ 时，$\lambda\boldsymbol{a} = \boldsymbol{0}$，当 $\lambda < 0$ 时，方向变为反向.
示例1:
在平行四边形$ABCD$中，两条对角线交于点$O$，求$\overrightarrow{OA} + \overrightarrow{OB} + 2\overrightarrow{OC}$.
画出图形.

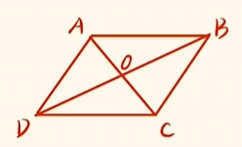
解 原式 $= \overrightarrow{OA} + \overrightarrow{DO} + 2\overrightarrow{OC} = \overrightarrow{DA} + 2\overrightarrow{OC} = \overrightarrow{DA} + \overrightarrow{AC} = \overrightarrow{DC}$.（或$\overrightarrow{AB}$）
示例2:

解 A. $\overrightarrow{AC} - \overrightarrow{AD} = \overrightarrow{DC} \neq \overrightarrow{AB}$.
B. $2(\overrightarrow{AC} - \overrightarrow{AD}) = 2\overrightarrow{DC} = \overrightarrow{BA} \neq \overrightarrow{AB}$.
C. $\overrightarrow{AD} - \overrightarrow{AC} = \overrightarrow{CD} \neq \overrightarrow{AB}$.
D. $2(\overrightarrow{AD} - \overrightarrow{AC}) = 2\overrightarrow{CD} = \overrightarrow{AB}$.
故选D.
示例3:

解 A. $\overrightarrow{AP} + \overrightarrow{SE} + \overrightarrow{RQ} = \overrightarrow{QC} + \overrightarrow{CR} + \overrightarrow{RQ} = \overrightarrow{QR} + \overrightarrow{RQ} = \vec{0}$.
B. 在正五边形$PQRST$中，有$PS \parallel QR$和$QT \parallel RS$，所以有平行四边形$APRT$，所以$\overrightarrow{AP} + \overrightarrow{AT} = \overrightarrow{AR}$.
左边 $= \overrightarrow{QC} + \overrightarrow{SD} = \overrightarrow{AP} + \overrightarrow{AT} = \overrightarrow{AR}$.
右边 $= \overrightarrow{QD} + \overrightarrow{RS} = \overrightarrow{BR} + \overrightarrow{RS} = \overrightarrow{BS}$.
因为$\overrightarrow{AR} \neq \overrightarrow{BS}$，所以左边$\neq$右边.
C. $AT = \dfrac{\sqrt{5} + 1}{2}PT = \dfrac{\sqrt{5} + 1}{2}TS$.
因为$\overrightarrow{AT} \parallel \overrightarrow{TS}$，所以$\overrightarrow{AT} = \dfrac{\sqrt{5} + 1}{2}\overrightarrow{TS}$.
D. 过点$A$作$AG \perp PT$于$G$点，则有$\mathrm{Rt}\triangle AGT$.

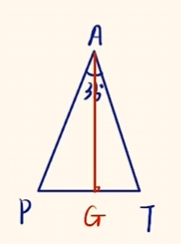
则$\angle GAT = 18 ^ \circ$，所以$\sin 18 ^ \circ = \dfrac{GT}{AT} = \dfrac{1}{2}\cdot\dfrac{PT}{AT} = \dfrac{\sqrt{5} - 1}{4}$.
由二倍角公式得$\cos 36 ^ \circ = 1 - 2\sin ^ 2 18 ^ \circ = 1 - 2(\dfrac{\sqrt{5} - 1}{4}) ^ 2 = \dfrac{\sqrt{5} + 1}{4}$.
故选ACD.

向量数量积

数量积

好比 $W = Fx\cos \theta$，向量的数量积

$$\boldsymbol{a} \cdot \boldsymbol{b} = |\boldsymbol{a}||\boldsymbol{b}| \cos \theta$$

其中，$\theta \in [0, \pi]$，并且可以用 $<\boldsymbol{a}, \boldsymbol{b}>$ 表示.
由此可得 $\cos \theta$ 的计算公式

$$\cos <\boldsymbol{a}, \boldsymbol{b}> = \cos \theta = \dfrac{\boldsymbol{a} \cdot \boldsymbol{b}}{|\boldsymbol{a}||\boldsymbol{b}|}$$

$\theta$ 大小和数量积的关系

  • $\theta \in [0, \dfrac{\pi}{2}) \implies \boldsymbol{a} \cdot \boldsymbol{b} > 0$
  • $\boldsymbol{a} \perp \boldsymbol{b} \implies \theta = \dfrac{\pi}{2} \implies \boldsymbol{a} \cdot \boldsymbol{b} = 0$
  • $\theta \in (\dfrac{\pi}{2}, \pi] \implies \boldsymbol{a} \cdot \boldsymbol{b} < 0$.


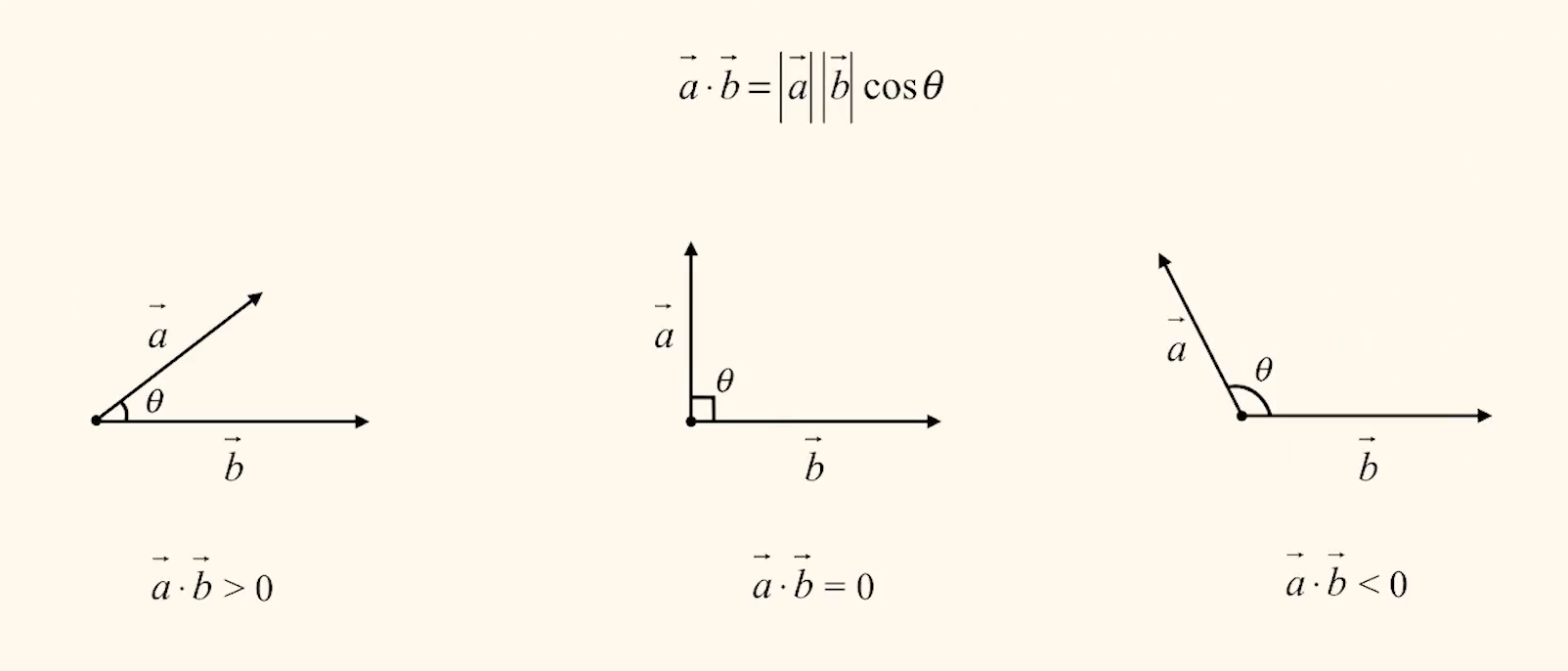
对于向量 $\boldsymbol{a}$，有 $\boldsymbol{a} \cdot \boldsymbol{a} = \boldsymbol{a}^2 = |\boldsymbol{a}|^2$，故

$$|\boldsymbol{a} \pm \boldsymbol{b}|^2 = (\boldsymbol{a} \pm \boldsymbol{b})^2 = \boldsymbol{a}^2 + \boldsymbol{b^2} \pm 2\boldsymbol{a} \cdot \boldsymbol{b}$$

因此，好比整式，如果已知 $\boldsymbol{a} + \boldsymbol{b}$ 和 $\boldsymbol{a} - \boldsymbol{b}$，那么就能求出 $\boldsymbol{a} \cdot \boldsymbol{b}$.

运算律

  1. 交换律
$$\boldsymbol{a} \cdot \boldsymbol{b} = \boldsymbol{b} \cdot \boldsymbol{a}$$
  1. 数乘结合律
$$(\lambda \boldsymbol{a}) \cdot \boldsymbol{b} = \lambda(\boldsymbol{a} \cdot \boldsymbol{b}) = \boldsymbol{a} \cdot (\lambda \boldsymbol{b})$$
  1. 分配律
$$(\boldsymbol{a} + \boldsymbol{b}) \cdot \boldsymbol{c} = \boldsymbol{a} \cdot \boldsymbol{c} + \boldsymbol{b} \cdot \boldsymbol{c}$$

投影向量


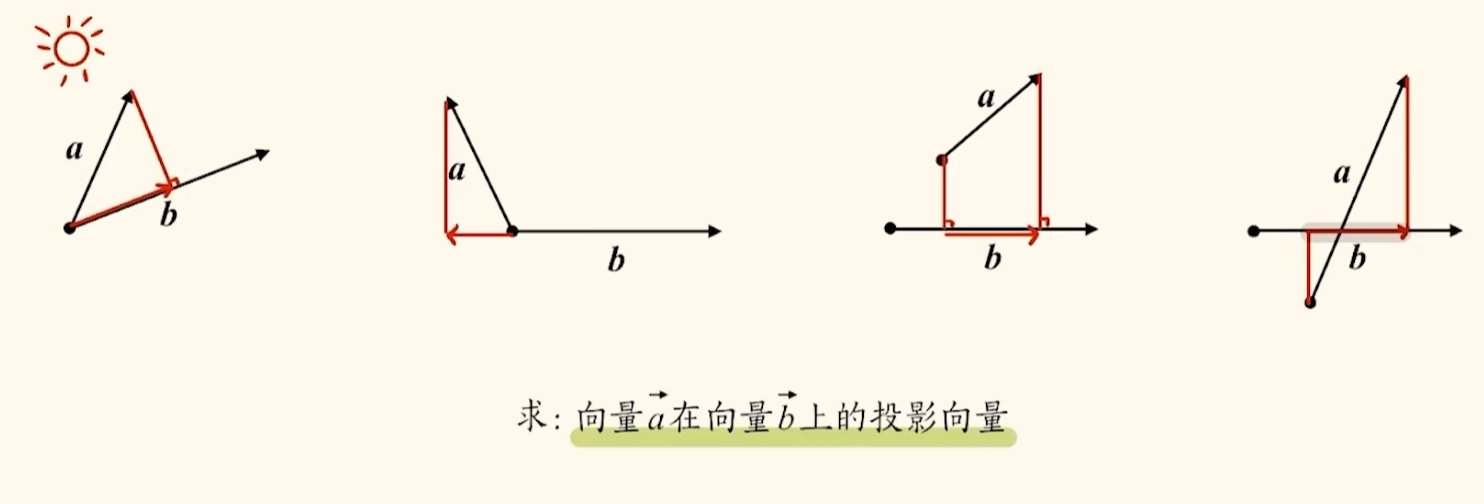
在向量 $\boldsymbol{b}$ 上，单位向量 $\boldsymbol{e}$ 的计算公式

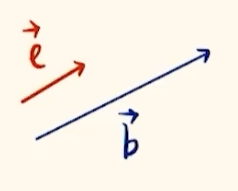
$$\boldsymbol{e} = \dfrac{\boldsymbol{b}}{|\boldsymbol{b}|}$$

在向量 $\boldsymbol{a}$ 与 $\boldsymbol{b}$ 中，已知两向量夹角 $\theta$，求 $\boldsymbol{a}$ 对 $\boldsymbol{b}$ 的投影向量 $\boldsymbol{m}$.

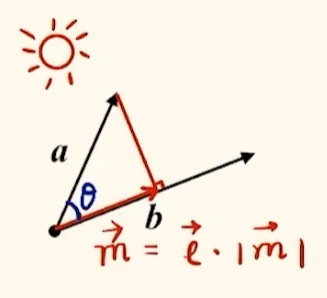
$ \begin{aligned} \boldsymbol{m} &= \boldsymbol{e} \cdot |\boldsymbol{m}| \\ &= \dfrac{\boldsymbol{b}}{|\boldsymbol{b}|} \cdot |\boldsymbol{a}| \cdot \cos \theta \\ &= \dfrac{\boldsymbol{b}}{|\boldsymbol{b}|} \cdot |\boldsymbol{a}| \cdot \dfrac{\boldsymbol{a} \cdot \boldsymbol{b}}{|\boldsymbol{a}||\boldsymbol{b}|} \\ &= \dfrac{\boldsymbol{a} \cdot \boldsymbol{b}}{|\boldsymbol{b}|^2}\boldsymbol{b} \end{aligned} $
则有公式

$$\boldsymbol{m} = \dfrac{\boldsymbol{a} \cdot \boldsymbol{b}}{|\boldsymbol{b}|^2}\boldsymbol{b}$$

基本定理


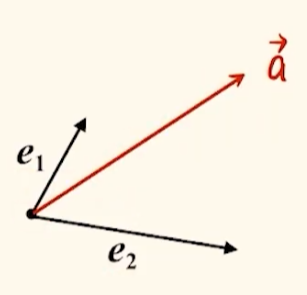
定理: 若 $\boldsymbol{e}_1$，$\boldsymbol{e}_2$ 是平面内两个不共线的向量，那么这对一平面内的任一向量 $\boldsymbol{a}$，有且只有一对实数 $\lambda_1$，$\lambda_2$，使得 $\boldsymbol{a} = \lambda_1\boldsymbol{e}_1 + \lambda_2\boldsymbol{e}_2$.
其中 $\{\boldsymbol{e}_1, \boldsymbol{e}_2\}$ 叫做表示这一平面内所有向量的一个基底.