不等式性质

加减乘除

$$a > b \implies \left\{ \begin{array}{lr} a + c > b + c \\ a \cdot c > b \cdot c \qquad (c > 0) \\ a \cdot c < b \cdot c \qquad (c < 0) \end{array} \right. $$

同向可加

$$\left\{ \begin{array}{lr} a > b \\ c > d \end{array} \right. \implies a + c > b + d $$

同向同正可乘

$$\left\{ \begin{array}{lr} a > b > 0 \\ c > d > 0 \end{array} \right. \implies a \cdot c > b \cdot d $$

正数乘方开方

$$a > b > 0 \implies \left\{ \begin{array}{lr} a ^ n > b ^ n \\ \sqrt[n]{a} > \sqrt[n]{b} \end{array} \right. \qquad (n > 0) $$

例题

选择题解题技巧:

不等式性质
化简选项
代入特殊值

示例1:

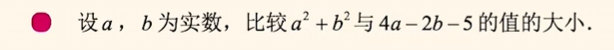
$ \begin{aligned} & \quad\; a^2 + b^2 - (4a - 2b - 5) \\ &= a^2 - 4a + b^2 + 2b + 5 \\ &= a^2 - 4a + 4 + b^2 + 2b + 1 \\ &= (a - 2)^2 + (b + 1)^2 \\ &\geq 0 \end{aligned} $
所以$a^2 + b^2 \geq 4a - 2b - 5$.

示例2:

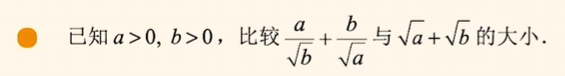
$ \begin{aligned} & \quad\; \dfrac{a}{\sqrt{b}} + \dfrac{b}{\sqrt{a}} - (\sqrt{a} + \sqrt{b}) \\ &= \dfrac{a\sqrt{a} + b\sqrt{b}}{\sqrt{ab}} - (\sqrt{a} + \sqrt{b}) \\ &= \dfrac{(\sqrt{a})^3 + (\sqrt{b})^3}{\sqrt{ab}} - (\sqrt{a} + \sqrt{b}) \\ &= \dfrac{(\sqrt{a} + \sqrt{b})(a + b - \sqrt{ab})}{\sqrt{ab}} - (\sqrt{a} + \sqrt{b}) \\ &= (\sqrt{a} + \sqrt{b})(\dfrac{a + b - \sqrt{ab}}{\sqrt{ab}} - 1) \\ &= (\sqrt{a} + \sqrt{b})(\dfrac{a + b - \sqrt{ab}}{\sqrt{ab}} - \dfrac{\sqrt{ab}}{\sqrt{ab}}) \\ &= (\sqrt{a} + \sqrt{b})(\dfrac{a + b - 2\sqrt{ab}}{\sqrt{ab}}) \\ &= (\sqrt{a} + \sqrt{b})[\dfrac{(\sqrt{a} - \sqrt{b})^2}{\sqrt{ab}}] \\ &\geq 0 \end{aligned} $
所以$\dfrac{a}{\sqrt{b}} + \dfrac{b}{\sqrt{a}} \geq \sqrt{a} + \sqrt{b}$.

示例3:

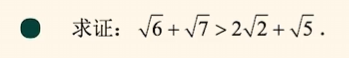
左边$^2 = 13 + 2\sqrt{42}$
右边$^2 = 13 + 2\sqrt{40}$
所以左边$>$右边.

示例4:

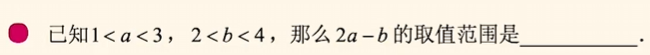
据题意
$ \left\{ \begin{array}{lr} 2 < 2a < 6 \\ -4 < -b < -2 \end{array} \right. \implies -2 < 2a - b < 4 $

示例5（通解）:

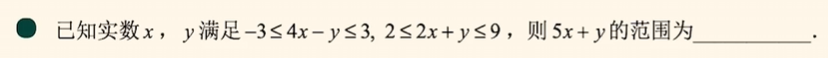
设$m = 4x - y$，$n = 2x + y$.
解得
$ \left\{ \begin{array}{lr} x = \dfrac{1}{6}(m + n) \\ y = \dfrac{2}{3}n - \dfrac{1}{3}m \end{array} \right. $
则$5x + y = \dfrac{1}{2}m + \dfrac{3}{2}n$.
所以$5x + y \in [\dfrac{3}{2}, 15]$.

含参二次不等式:

基本不等式

由$(\sqrt{x} - \sqrt{y})^2 \geq 0$得

$$\boldsymbol{x + y \geq 2\sqrt{xy} \qquad (x, y \geq 0)} $$

注意: 当$x + y = 2\sqrt{xy}$时，$x = y$，应验证等号是否成立.

例题

和积式
非齐次式

求$(2x + \dfrac{1}{x - 1})_{min} \qquad (x > 0)$.
$ \begin{aligned} 原式 &= 2x - 2 + \dfrac{1}{x - 1} + 2 \\ &\geq 2\sqrt{(2x - 2) \cdot \dfrac{1}{x - 1}} + 2 \\ &= 2\sqrt{2} + 2 \end{aligned} $
所以$(2x + \dfrac{1}{x - 1})_{min} = 2\sqrt{2} + 2$.

齐次式
齐次式: 分子分母每项次数都相同.

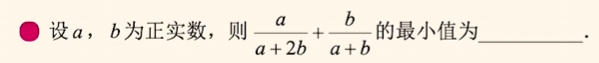
设
$ \left\{ \begin{array}{lr} m = a + 2b \\ n = a + b \end{array} \right. $
则
$\begin{aligned} &\quad\; \dfrac{a}{a + 2b} + \dfrac{b}{a + b} \\ &= \dfrac{2n - m}{m} + \dfrac{m - n}{n} \\ &= \dfrac{2n}{m} + \dfrac{m}{n} - 1 - 1 \\ &\geq 2\sqrt{2} - 2 \end{aligned} $

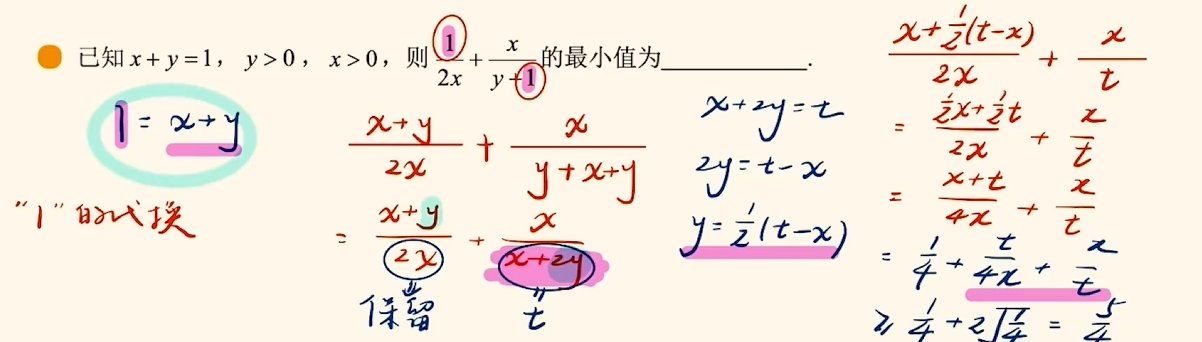
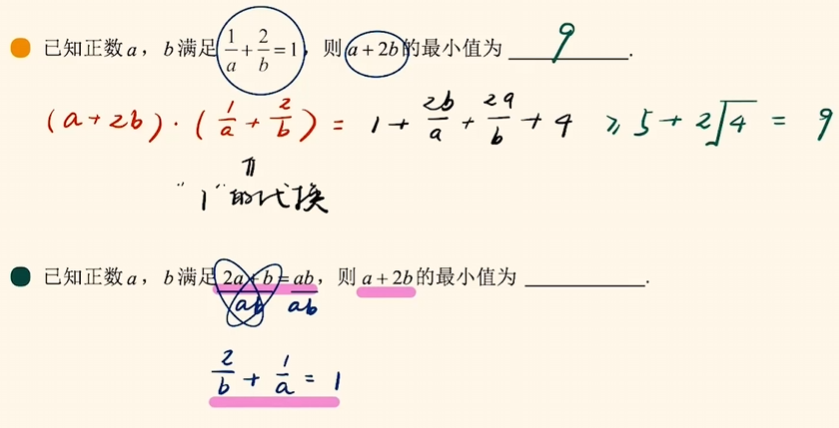
进阶

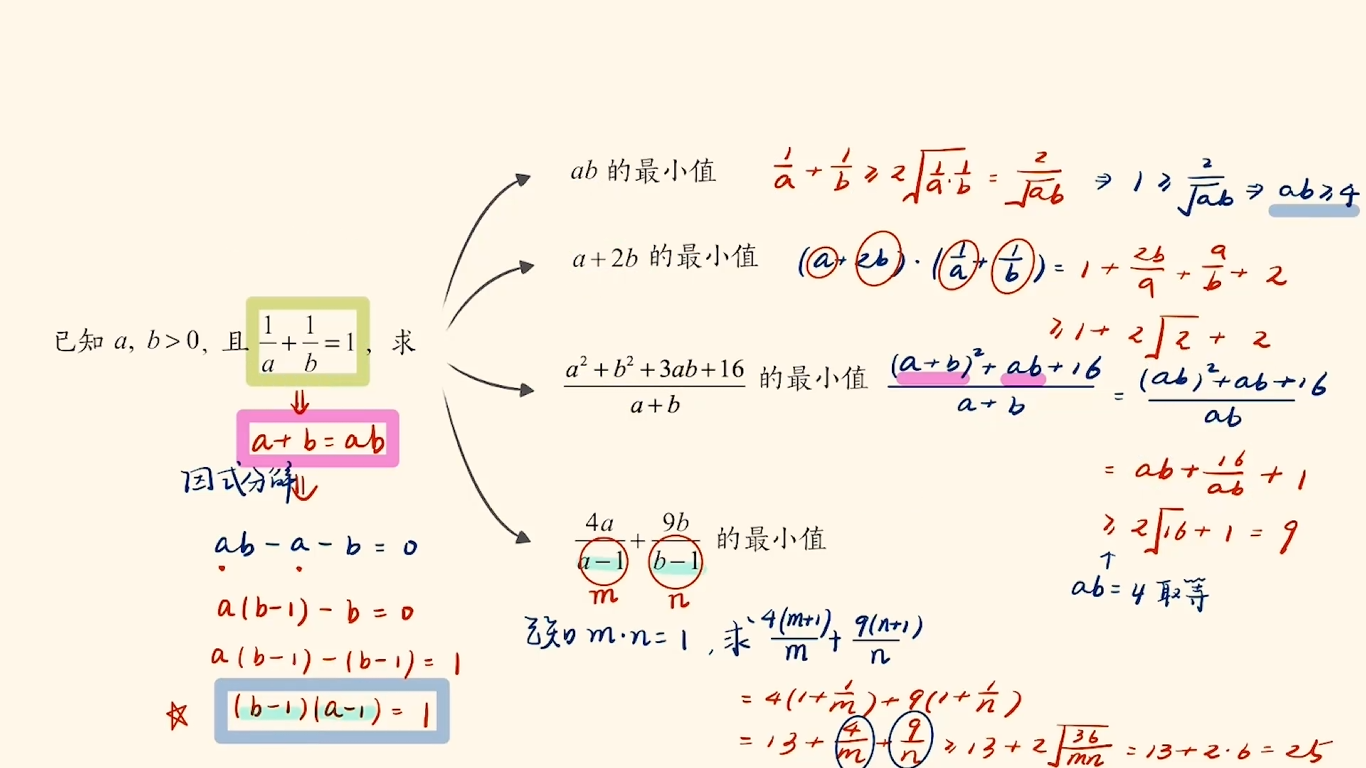
换元法

凑其次

强行消元

多次使用不等式

元的个数$=$方程个数$=$不等式使用次数.

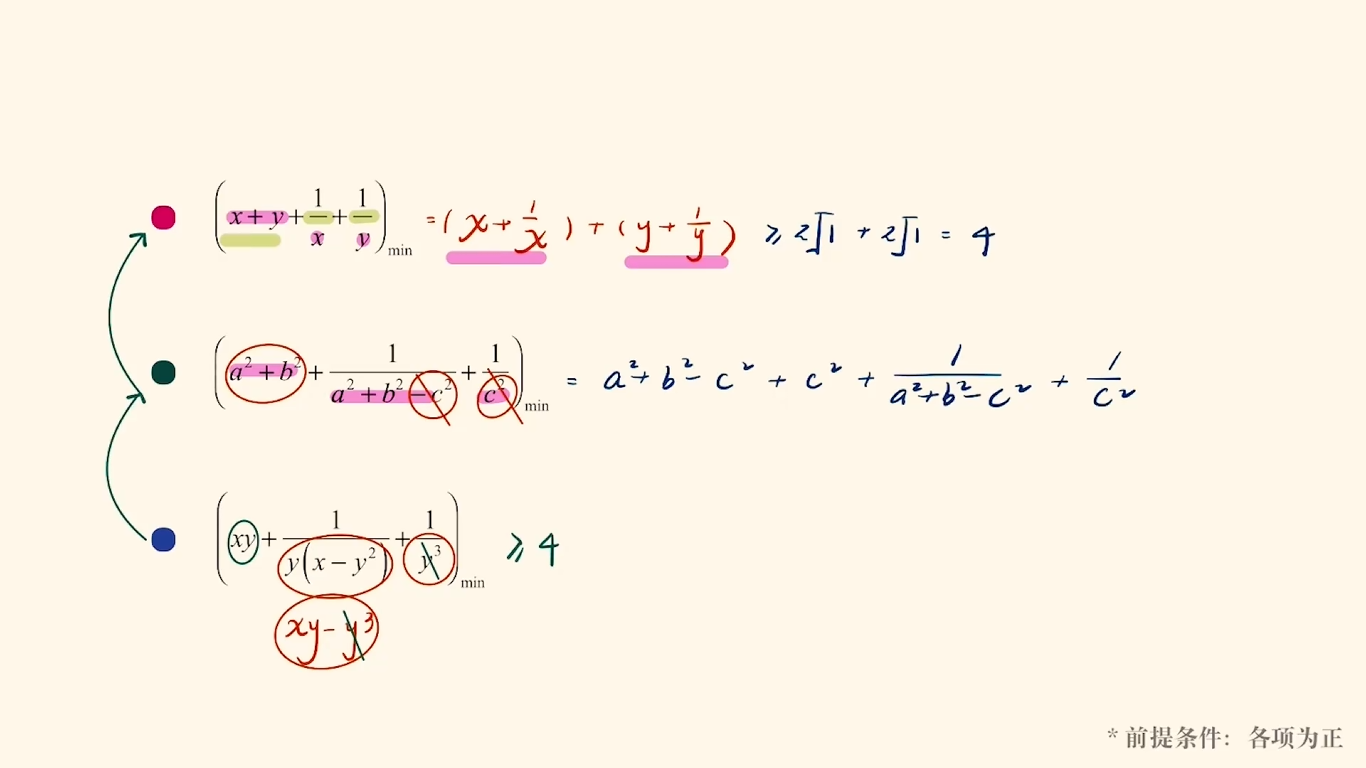
设$a > b > c > 0$，求$2a^2 + \dfrac{1}{ab} + \dfrac{1}{a(a - b)} - 10ac + 25c^2$的最小值.
$ \begin{aligned} & \quad\; 2a^2 + \dfrac{1}{ab} + \dfrac{1}{a(a - b)} - 10ac + 25c^2 \\ &= a^2 - 10ac + 25c^2 + a^2 + \dfrac{1}{ab} + \dfrac{1}{a(a - b)} \\ &= (a - 5c)^2 + a^2 + \dfrac{1}{a^2 - ab} + \dfrac{1}{ab} \\ &= (a - 5c)^2 + a^2 - ab + \dfrac{1}{a^2 - ab} + ab + \dfrac{1}{ab} \\ &\geq (a - 5c)^2 + 2\sqrt{1} + 2\sqrt{1} \\ &= (a - 5c)^2 + 4 \\ &\geq 4 \end{aligned} $