函数初步
概念
函数用 $f(x)$ 表示.
复合函数: 形如 $f(g(x))$ 的函数,$f(g(x)) \neq g(f(x))$.
函数三要素: 定义域、值域、对应法则.
求定义域
求具体函数定义域
- 分式: 分母 $\neq 0$.
- 根式: 根号下式 $\geq 0$.
- $0$ 次幂: 底数 $\neq 0$.
- 正切值: $\tan x$ 中,$x \neq k\pi + \dfrac{\pi}{2}$.
- 对数: $\log_a x$ 中,$x > 0$.
求抽象函数定义域
在 $f(a)$ 和 $f(b)$ 中,自变量取值范围一致,即如果 $a \in M$,则 $b \in M$.
求函数解析式
待定系数法
当题目中写明函数类型时,使用待定系数法,如设 $f(x) = kx + b$ 或 $f(x) = ax^2 + bx + c$ 等.
换元法
当题目中的函数自变量较为复杂时,使用换元法,设题目中的自变量为一个未知量,把自变量用未知量表示出来.
示例: 已知 $f(\sqrt{x} + 1) = 2x + 1$,求 $f(x)$.
设 $m = \sqrt{x} + 1$,得 $x = m^2 - 2m + 1$.
则 $f(m) = 2m^2 - 4m + 3$.
所以 $f(x) = 2x^2 - 4x + 3$.
因为 $\sqrt{x} + 1 \geq 1$,
所以 $f(x) = 2x^2 - 4x + 3$,$x \in [1, +\infty)$.
整体代换法
当题目中的函数自变量较为复杂且换元法难以计算时,观察自变量与函数解析式的关系,使用整体代换.
示例: 已知 $f(x - \dfrac{1}{x}) = x^2 + \dfrac{1}{x^2}$,求 $f(0)$ 和 $f(x)$.
注意到 $(x - \dfrac{1}{x})^2 = x^2 + \dfrac{1}{x^2} - 2$.
所以 $f(x - \dfrac{1}{x}) = (x - \dfrac{1}{x})^2 + 2$.
则 $f(x) = x^2 + 2$,所以 $f(0) = 2$.
构造方程组
当题目条件中出现不同自变量的同一函数时,构造方程组.
示例1: 已知定义域为 $\mathbb{R}$ 的函数 $f(x)$ 满足 $2f(x) - f(-x) = 3x^3$,求 $f(x)$.
已知 $2f(x) - f(-x) = 3x^3$. $(1)$
对上式变形得 $2f(-x) - f(-(-x)) = 3(-x)^3$.
化简得 $2f(-x) - f(x) = -3x^3$. $(2)$
联立 $(1)(2)$ 得
$
\left\{
\begin{array}{lr}
2f(x) - f(-x) = 3x^3 \qquad\;\;\, (1)\\
2f(-x) - f(x) = -3x^3 \qquad (2)
\end{array}
\right.
$
解得 $f(x) = x^3$.
含参分段函数
示例: 设函数 $f(x) = \left\{ \begin{array}{lr} x^2 + 2x, x \leq 0 \\ -x^2, x > 0 \end{array} \right.$,若 $f(f(a)) - f(a) + 2 = 0$,求实数 $a$ 的值.
设 $m = f(a)$.
则原式变形为 $f(m) - m + 2 = 0$.
方法一: 使用分类讨论思想.
- 当 $m \leq 0$ 时,
$m^2 + 2m - m + 2 = 0$.
$m^2 + m + 2 = 0$.
$\Delta = -7 < 0$,此时方程无解. - 当 $m > 0$ 时,
$-m^2 - m + 2 = 0$.
解得 $m_1 = -2$(舍去),$m_2 = 1$.
综上,$m = 1$.
- 当 $a \leq 0$ 时,
$a^2 + 2a = 1$.
$a^2 + 2a - 1 = 0$.
解得 $a_1 = -1 + \sqrt{2}$(舍去),$a_2 = -1 - \sqrt{2}$. - 当 $a > 0$ 时,
$-a^2 = 1$.
方程无解.
综上所述,$a = -1 - \sqrt{2}$.
方法二: 画图法.
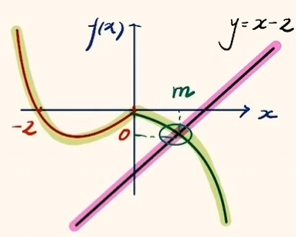
计算后显然 $m = 1$.
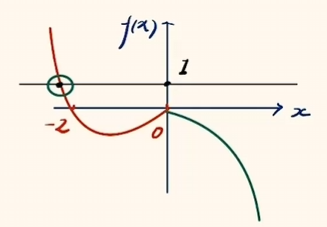
计算后显然 $a = -1 - \sqrt{2}$.
分式函数求值域
一次比一次
示例: 已知函数 $f(x) = \dfrac{2x - 3}{x + 1}$,$x \in [1, +\infty)$,求函数的值域.
由 $x + 1 \neq 0$ 得,竖直方向渐近线为直线 $x = -1$.
由 $\lim\limits_{x \to \infty} f(x) = 2$ 得,水平方向渐近线为直线 $y = 2$.
画出可能的图象.
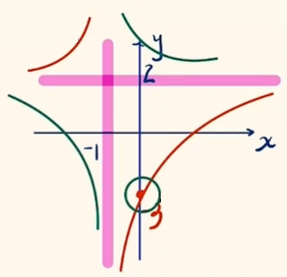
函数截距为 $f(0) = -3$,则保留正确的图象.
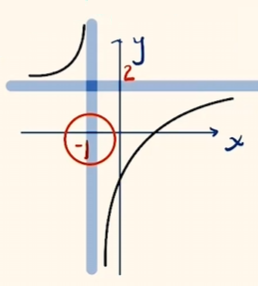
则对于 $x \in [1, +\infty)$,函数值域为 $f(x) \in [-\dfrac{1}{2}, 2)$.
二次比一次
对勾函数与双刀函数: 形如 $f(x) = ax + \dfrac{b}{x}$ 的函数.
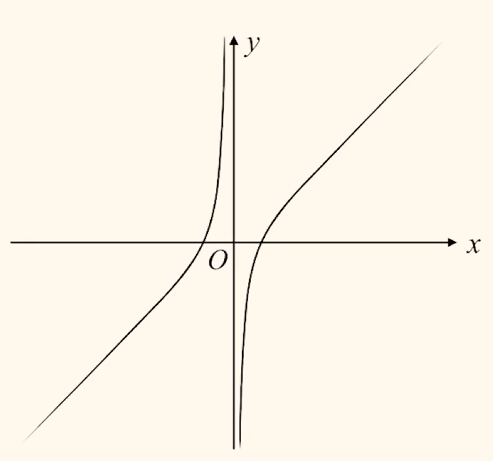
对勾函数: 已知函数 $f(x) = ax + \dfrac{b}{x} \; (a > 0, b > 0)$,则图象为
渐近线为直线 $x = 0$ 和直线 $y = ax$.
在第一象限中,由基本不等式 $f(x) = ax + \dfrac{b}{x} \geq 2\sqrt{x \cdot \dfrac{ab}{x}} = 2\sqrt{ab}$ 得,图象最低点纵坐标为 $2\sqrt{ab}$.
此时 $ax = \dfrac{b}{x}$,得 $x = \sqrt{\dfrac{b}{a}} = \dfrac{\sqrt{ab}}{a}$,即最低点坐标 $(\dfrac{\sqrt{ab}}{a}, 2\sqrt{ab})$.
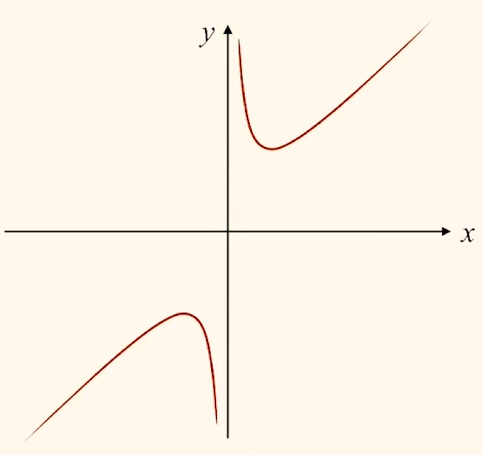
对勾函数: 已知函数 $f(x) = ax + \dfrac{b}{x} \; (a > 0, b < 0)$,则图象为
示例1: 已知函数 $f(x) = \dfrac{x^2 + 2x + 3}{x}$,$x \in [2, +\infty)$,求函数的值域.
化简得 $f(x) = x + \dfrac{3}{x} + 2$.
画出 $f(x) = x + \dfrac{3}{x}$ 的图象,可求得第一象限最低点 $(\sqrt{3}, 2\sqrt{3})$.
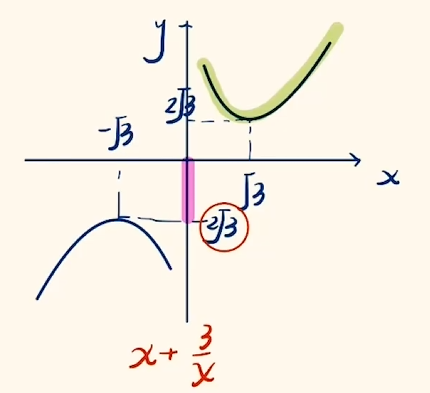
向上平移 $2$ 个单位,得到 $f(x) = x + \dfrac{3}{x} + 2$ 的图象.
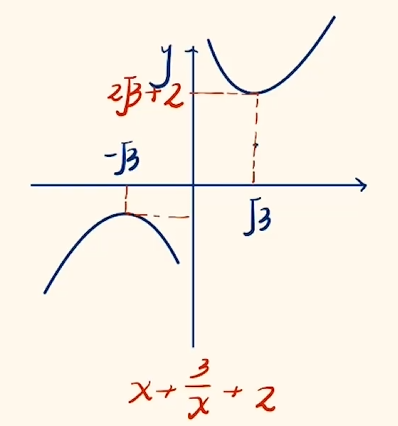
计算出 $f(2) = \dfrac{11}{2}$.
所以 $f(x) \in [\dfrac{11}{2}, +\infty)$.
示例2:

二次比二次
凑分母: 把分子凑为分母倍数.
示例: 已知函数 $f(x) = \dfrac{2x^2 + 9x + 13}{x^2 + 4x + 6}$,$x \in [0, 1]$,求函数的值域.
函数变形为 $f(x) = \dfrac{2(x^2 + 4x + 6) + x + 1}{x^2 + 4x + 6} = \dfrac{x + 1}{x^2 + 4x + 6} + 2$.
设 $m = x + 1$,则 $f(x) = \dfrac{m}{m^2 + 2m + 3} + 2 = \dfrac{1}{m + \dfrac{3}{m} + 2} + 2$.
因为 $m \in [1, 2]$,所以 $m + \dfrac{3}{m} \in [2\sqrt{3}, 4]$.
所以 $m + \dfrac{3}{m} + 2 \in [2\sqrt{3} + 2, 6]$.
所以 $\dfrac{1}{m + \dfrac{3}{m} + 2} \in [\dfrac{1}{6}, \dfrac{1}{2\sqrt{3} + 2}]$.
所以 $f(x) \in [\dfrac{13}{6}, \dfrac{1}{2\sqrt{3} + 2} + 2]$.
化简得 $\ldots$
恒成立问题
准备: 学会使用初中方法求二次函数在给定区间上的最值.
恒成立问题可以转化为求最值问题:
$\forall x,\; f(x) > a \iff f(x)_{\mathrm{min}} > a$.
$\forall x,\; f(x) < a \iff f(x)_{\mathrm{max}} < a$.
示例1: $\forall x \in [2, 3],\; x^2 - ax + 2 \geq 0$,求 $a$ 的取值范围.
分类讨论
转化为: 在 $2 \leq x \leq 3$ 中,$x^2 - ax + 2$ 最小值总大于 $0$,求 $a$ 的取值范围.
$f(x) = x^2 - ax + 2$ 的对称轴为直线 $x = \dfrac{a}{2}$.
- 当 $\dfrac{a}{2} \in (2, 3)$ 时:
$f(x)_{\mathrm{min}} = f(\dfrac{a}{2}) \geq 0$.
则 $\dfrac{a^2}{4} - \dfrac{a^2}{2} + 2 \geq 0$.
解得 $a \in [-2\sqrt{2}, 2\sqrt{2}]$.
因为 $\dfrac{a}{2} \in (2, 3)$,
所以此时不存在 $a$. - 当 $\dfrac{a}{2} \in (-\infty, 2]$ 时:
$f(x)_{\mathrm{min}} = f(2) \geq 0$.
则 $6 - 2a \geq 0$.
解得 $a \in (-\infty, 3]$.
因为 $\dfrac{a}{2} \in (-\infty, 2]$,
所以 $a \in (-\infty, 3]$ - 当 $\dfrac{a}{2} \in [3, +\infty)$ 时:
$f(x)_{\mathrm{min}} = f(3)$.
则 $11 - 3a \geq 0$.
因为 $\dfrac{a}{2} \in [3, +\infty)$.
所以此时不存在 $a$.
综上,$a \in (-\infty, 3]$.
必要探路
显然 $f(2) = 4 - 2a + 2 \geq 0$ 成立.
则 $a \leq 3$.
则对称轴直线 $x = \dfrac{a}{2} \leq \dfrac{3}{2}$.
则只可能存在分类讨论中的第二种情况.
则 $a \in (-\infty, 3]$.
示例2: $\forall x \in [-2, -1],\; -2 \leq x^2 + (a + 1)x - a \leq 2$,求实数 $a$ 的取值范围.
显然 $-2 \leq f(-2) \leq 2 \implies a \in [0, \dfrac{4}{3}]$;
显然 $-2 \leq f(-1) \leq 2 \implies a \in [-1, 1]$.
则对称轴直线 $x = -\dfrac{a + 1}{2} \in [-1, -\dfrac{1}{2}]$.
所以对称轴必在点 $(-1, 0)$ 右边.
又因为函数开口向上,
所以函数在 $[-2, -1]$ 上单调递减.
则 $f(-1) \geq -2$ 且 $f(-2) \geq 2$.
所以 $a \in [0, 1]$.
分离参数
因为 $x^2 - ax + 2 \geq 0$,
所以 $a \leq x + \dfrac{2}{x}$.
则 $a \leq (x + \dfrac{2}{x})_{\mathrm{min}}$.
因为 $x + \dfrac{2}{x} \geq 2\sqrt{2}$,
又因为 $x \in [2, 3]$,
所以当 $x = 2$ 时,有 $(x + \dfrac{2}{x})_{\mathrm{min}} = 3$.
则 $a \leq 3$.
示例2: $\forall x \in [2, 4],\; x^2 - ax \geq 4x + a - 3$,求 $a$ 的取值范围.
据题意,$a \leq \dfrac{x^2 - 4x + 3}{x + 1}$.
设 $m = x + 1$,则 $m \in [3, 5]$.
则 $a \leq \dfrac{m^2 - 6m + 8}{m} = m + \dfrac{8}{m} - 6$.
因为 $m + \dfrac{8}{m} \geq 4\sqrt{2}$,此时 $m = 2\sqrt{2}$,
又因为 $m \in [3, 5]$,
所以当 $m = 3$ 时,有 $(m + \dfrac{8}{m})_{\mathrm{min}} = \dfrac{17}{3}$.
所以 $a \leq \dfrac{17}{3} - 6 = -\dfrac{1}{3}$.
即 $a \in (-\infty, -\dfrac{1}{3}]$.
单调性
概念
标准定义:
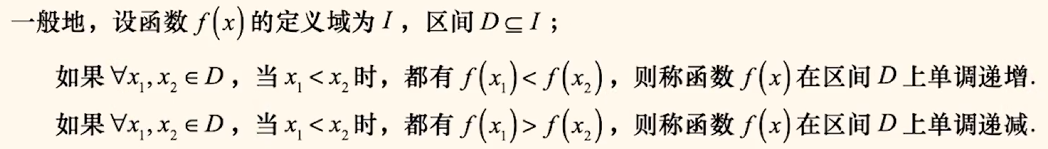
适用于利用定义判断单调性.
理解:
在区间 $D$ 内,函数 $f(x)$ 随 $x$ 的增大而增大,则称该函数 $f(x)$ 在区间 $D$ 内单调递增,则 $x_1 > x_2 \iff f(x_1) > f(x_2)$.
在区间 $D$ 内,函数 $f(x)$ 随 $x$ 的增大而减小,则称该函数 $f(x)$ 在区间 $D$ 内单调递减,则 $x_1 > x_2 \iff f(x_1) < f(x_2)$.
增函数: 在定义域中单调递增;减函数: 在定义域中单调递减.
示例: 函数 $f(x) = \dfrac{1}{x}$ 的单调减区间为 $(-\infty, 0)$,$(0, +\infty)$.
函数 $f(x) = x + \dfrac{1}{x}$ 的单调增区间为 $(-\infty, -1)$,$(1, +\infty)$;单调减区间为 $(-1, 0)$,$(0, 1)$.
(其中部分端点既可以使用开区间,也可以使用开区间,推荐使用开区间)
单调性的三种表达方式:
-
当 $x_1 > x_2$ 时,$f(x_1) > f(x_2)$ 恒成立.
即 $f(x)$ 是增函数. -
$(x_1 - x_2)[f(x_1) - f(x_2)] > 0$.
由不等式可得 $x_1 > x_2$ 且 $f(x_1) > f(x_2)$.(或 $x_1 < x_2$ 且 $f(x_1) < f(x_2)$)
则 $f(x)$ 是增函数. -
$\dfrac{f(x_1) - f(x_2)}{x_1 - x_2} > 0$.
该式等价于 $(x_1 - x_2)[f(x_1) - f(x_2)] > 0$.
故 $f(x)$ 是增函数.
单调性判断
普通简单函数
使用画图法.
示例: 函数 $f(x) = x^2 + ax + 2$ 在 $[3, +\infty)$ 上单调递增,求实数 $a$ 的取值范围.
即初中问题: 函数 $y = x^2 + ax + 2$ 在 $x \geq 3$ 时随 $x$ 的增大而增大,求实数 $a$ 的取值范围.
据题意 $-\dfrac{a}{2} \leq 3$.
所以 $a \in [-6, +\infty)$.
分段函数
示例1: 已知函数 $f(x) = \left\{ \begin{array}{lr} (2a - 1)x + a,\; x < 1 \\ -ax,\; x \geq 1 \end{array} \right.$ 是定义在 $(0, +\infty)$ 的减函数,求实数 $a$ 的取值范围.
据题意 $\left\{ \begin{array}{lr} 2a - 1 < 0 \\ -a < 0 \\ (2a - 1) \cdot 1 + a \geq -a \cdot 1 \end{array} \right.$
解得 $a \in [\dfrac{1}{4}, \dfrac{1}{2})$.
示例2: 已知函数 $f(x) = \left\{ \begin{array}{lr} x^2 - ax + 5,\; x \leq 1 \\ \dfrac{a}{x},\; x > 1 \end{array} \right.$ 满足 $\forall x_1 \neq x_2,\; (x_2 - x_1)[f(x_2) - f(x_1)] < 0$,求实数 $a$ 的取值范围.
据题意,$f(x)$ 是减函数.
画图.
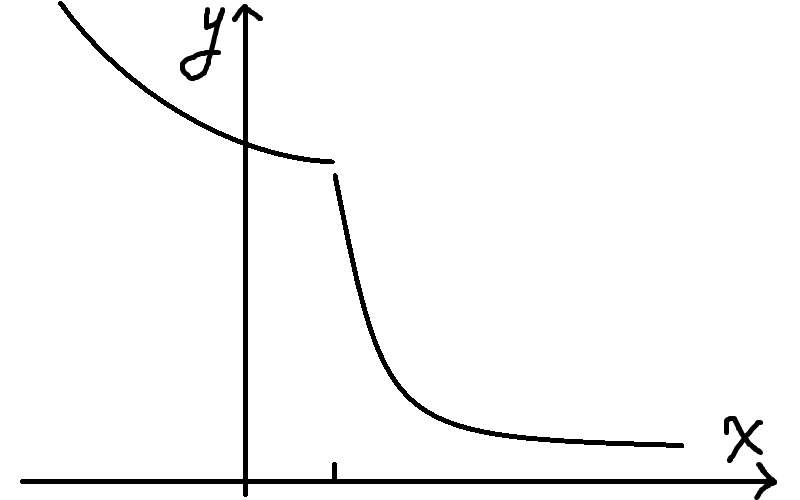
则 $\left\{ \begin{array}{lr} a > 0 \\ -\dfrac{-a}{2} \geq 1 \\ 1 - a + 5 \geq a \end{array} \right.$
所以 $a \in [2, 3]$.
利用定义证明
- 设 $x_1 < x_2$ 或 $x_1 > x_2$.
- 做差: $f(x_1) - f(x_2)$.
- 因式分解.
示例: 试利用定义证明函数 $f(x) = x + \dfrac{1}{x}$ 在 $x \in (0, 1)$ 上是减函数,在 $x \in (1, +\infty)$ 上是增函数.
设 $x_1 < x_2$,则
$
\begin{aligned}
& \quad\; f(x_1) - f(x_2) \\
&= x_1 + \dfrac{1}{x_1} - x_2 - \dfrac{1}{x_2} \\
&= (x_1 - x_2) + (\dfrac{1}{x_1} - \dfrac{1}{x_2}) \\
&= (x_1 - x_2) + (\dfrac{x_2 - x_1}{x_1x_2}) \\
&= (x_1 - x_2) - (\dfrac{x_1 - x_2}{x_1x_2}) \\
&= (x_1 - x_2)(1 - \dfrac{1}{x_1x_2}) \\
&= (x_1 - x_2)(\dfrac{x_1x_2 - 1}{x_1x_2})
\end{aligned}
$
- 当 $x \in (0, 1)$ 时:
因为 $0 < x_1 < x_2 < 1$,
所以 $x_1 - x_2 < 0$,$0 < x_1x_2 < 1$,$x_1x_2 - 1 < 0$.
所以原式 $> 0$.
则 $f(x_1) > f(x_2)$.
又因为 $x_1 < x_2$,
所以函数 $f(x) = x + \dfrac{1}{x}$ 在 $x \in (0, 1)$ 上是减函数. - 当 $x \in (1, +\infty)$ 时:
因为 $1 < x_1 < x_2$,
所以 $x_1 - x_2 < 0$,$0 < 1 < x_1x_2$.
所以原式 $< 0$.
则 $f(x_1) < f(x_2)$.
又因为 $x_1 < x_2$,
所以函数 $f(x) = x + \dfrac{1}{x}$ 在 $x \in (1, +\infty)$ 上是增函数.
复合函数
循序渐进推理.
示例1: $f(x) = -\dfrac{1}{\sqrt{2x + 1}}$.
$x \nearrow$,$2x + 1 \nearrow$,$\sqrt{2x - 1} \nearrow$,$\dfrac{1}{\sqrt{2x + 1}} \searrow$,$-\dfrac{1}{\sqrt{2x + 1}} \nearrow$.
故 $f(x)$ 在 $(-\dfrac{1}{2}, +\infty)$ 上单调递增.
示例2: 求 $g(x) = \sqrt{-x^2 + 2x + 15}$ 的单调增区间.
据题意,$-(x - 5)(x + 3) \geq 0$.
故开口向下,与 $x$ 轴交点为 $(5, 0)$ 与 $(-3, 0)$.
对称轴为直线 $x = 1$.
故单调增区间为 $(-3, 1)$.
利用单调性解不等式
基础问题
示例1: 已知定义在 $[0, +\infty)$ 上的单调减函数 $f(x)$,若 $f(2a - 1) > f(\dfrac{1}{3})$,求 $a$ 的取值范围.
因为 $f(x)$ 是定义在 $[0, +\infty)$ 上的单调减函数,
所以 $0 < 2a - 1 < \dfrac{1}{3}$.
解得 $a \in (\dfrac{1}{2}, \dfrac{2}{3})$.
示例2: 定义在 $\mathbb{R}$ 上的函数 $f(x)$ 满足: 对任意的 $x_1$,$x_2 \in [1, +\infty) \; (x_1 \neq x_2)$,有 $\dfrac{f(x_2) - f(x_1)}{x_2 - x_1} < 0$,则
A. $f(3) < f(2) < f(4)$.
B. $f(1) < f(2) < f(3)$.
C. $f(2) < f(1) < f(3)$.
D. $f(3) < f(1) < f(0)$.
据题意,$f(x)$ 在区间 $[1, +\infty)$ 上单调递减.
故选D.
函数不等式问题综合
奇偶性
概念
偶函数: 关于 $y$ 轴对称的函数,即 $f(x) = f(-x)$.
奇函数: 关于原点对称的函数,即 $f(x) = -f(-x)$.
非奇非偶: 非奇函数也非偶函数.
即奇又偶: $x$ 轴.(直线 $y = 0$)
其中奇偶函数定义域必须对称,即定义域为 $(a, b)$ 是,必有 $a = b$,适用于已知奇偶性求参数.
常见结论
常见奇偶函数
常见奇函数:
- $f(x) = x^{2k + 1}$,$k \in \mathbb{Z}$.
- $f(x) = ax \pm \dfrac{b}{x}$.
常见偶函数:
- $f(x) = x^{2k}$,$k \in \mathbb{Z}$.
- $f(x) = |x|$.
加减乘除
(奇 $=$ 奇函数,偶 $=$ 偶函数,非 $=$ 非奇非偶函数,其中乘号可以换成除号)
- 奇 $+$ 奇 $=$ 奇.
- 奇 $\times$ 奇 $=$ 偶.
- 奇 $\times$ 偶 $=$ 奇.
- 奇 $+$ 偶 $=$ 非.
对于2.的证明:
已知 $f(x)$,$g(x)$ 是奇函数,求证 $f(x) \cdot g(x)$ 是偶函数.
令 $h(x) = f(x) \cdot g(x)$.
则 $h(-x) = f(-x) \cdot g(-x)$.
因为 $f(x)$,$g(x)$ 是奇函数,所以 $f(-x) = -f(x)$,$g(-x) = -g(x)$.
所以 $h(-x) = f(x) \cdot g(x) = h(x)$.
所以 $f(x) \cdot g(x)$ 是偶函数.
奇函数的 $f(0)$
在原点处有定义的奇函数 $f(0) = 0$.
适用于已知奇偶性求参数.
判断奇偶性
- 看定义域是否对称,如果不对称,则函数非奇非偶.
- 看图象(如果能画出)或比较 $f(x)$ 与 $f(-x)$.
示例:
-
$f(x) = x^2$,$x \in (-1, 1]$.
因为 $x \in (-1, 1]$,
所以 $f(x)$ 非奇非偶. -
$f(x) = \sqrt{1 - x^2} + \sqrt{x^2 - 1}$.
据题意 $\left\{ \begin{array}{lr} 1 - x^2 \geq 0 \\ x^2 - 1 \geq 0 \end{array} \right.$
解得 $x^2 = 1$.
所以 $x = \pm 1$.
因为 $f(-1) = f(1) = 0$,
所以 $f(x)$ 既奇又偶. -
$f(x) = \sqrt{\dfrac{1 + x}{1 - x}} \cdot (x - 1)$.
据题意,$(1 + x)(1 - x) \geq 0$ 且 $x \neq 1$.
解得 $x \in [-1, 1)$.
所以 $f(x)$ 非奇非偶. -
$f(x) = \dfrac{|x^3 + x|}{\sqrt{x^2 - 1}}$.
据题意,$x^2 - 1 > 0$.
解得 $x \in (-\infty, -1) \cup (1, +\infty)$.
$ \begin{aligned} f(-x) &= \dfrac{|(-x)^3 + (-x)|}{\sqrt{(-x)^2 - 1}} \\ &= \dfrac{|-x^3 - x|}{\sqrt{x^2 - 1}} \\ &= \dfrac{|x^3 + x|}{\sqrt{x^2 - 1}} \\ &= f(x) \end{aligned} $
所以 $f(x)$ 是奇函数.
已知奇偶性求参数
方法一: 证明 $f(x)$ 与 $f(-x)$ 的关系.(大题中使用)
方法二: 代入特殊值.(推荐)
方法三: 定义域必定关于原点对称.
示例1: 已知 $f(x) = (3x + 1)(x - a)(3x - 1)$ 是奇函数,求 $a$ 的值.
因为 $f(x)$ 是奇函数,
所以 $f(0) = 1 \cdot (-a)(-1) = a = 0$.
示例2: 函数 $g(x) = (3ax^2 - \dfrac{2}{x} - x)^5$ 为奇函数,求 $a$ 的值.
因为 $g(x)$ 为奇函数,
所以 $g(1) = -g(-1)$.
则 $3a - 3 = -3a - 1$.
解得 $a = \dfrac{1}{3}$.
示例3: 函数 $f(x) = ax^2 + bx + 1$ 是偶函数,且定义域是 $[a - 6, 2a]$,求 $a + b$.
因为 $f(x)$ 是偶函数,
所以 $a - 6 = 2a$.
所以 $a = -6$.
所以 $f(x) = -6x^2 + bx + 1$.
因为 $f(x)$ 是偶函数,
所以 $f(1) = f(-1)$.
则 $-5 + b = -5 - b$.
所以 $b = 0$.
所以 $a + b = -6$.
示例4: 若 $f(x) = \dfrac{x}{(x - 1)(3x + a)}$ 是奇函数,求 $a$ 的值.
据题意,$x \neq 1$ 且 $x \neq -\dfrac{a}{3}$.
由定义域关于原点对称得 $-\dfrac{a}{3} = -1$.
所以 $a = 3$.
已知奇偶性求解析式
- 求一定义域内的解析式,则设 $x$ 在该定义域内.
- 多个函数相加,则变换 $x$ 为 $-x$.
示例1: 已知定义在 $\mathbb{R}$ 上的奇函数,已知 $x > 0$,$f(x) = x^2 + \dfrac{1}{x} + 2$,求该函数解析式.
设 $x < 0$.
则 $-x > 0$.
则 $f(x) = -f(-x) = -[(-x)^2 + \dfrac{1}{-x} + 2] = -[x^2 - \dfrac{1}{x} + 2] = -x^2 + \dfrac{1}{x} - 2$.
所以函数解析式为 $f(x) = \left\{ \begin{array}{lr} x^2 + \dfrac{1}{x} + 2,\; x > 0 \\ 0,\; x = 0 \\ -x^2 + \dfrac{1}{x} - 2,\; x < 0 \end{array} \right.$
示例2: 已知函数 $f(x)$ 和 $g(x)$ 分别是偶函数和奇函数,且 $f(x) + g(x) = \dfrac{1}{x - 1}$,求 $f(x)$ 的解析式.
因为函数 $f(x)$ 和 $g(x)$ 分别是偶函数和奇函数,
所以 $f(-x) + g(-x) = f(x) - g(x) = \dfrac{1}{-x - 1}$.
则 $\left\{ \begin{array}{lr} f(x) + g(x) = \dfrac{1}{x - 1} \\ f(x) - g(x) = \dfrac{1}{-x - 1} \end{array} \right.$
解得 $f(x) = \dfrac{1}{2} \cdot (\dfrac{1}{x - 1} - \dfrac{1}{x + 1})$.
函数不等式问题综合
- 先看奇偶性.
- 再看单调性.
示例1: 设函数 $f(x) = x^2 - \dfrac{1}{x^2 + 1}$,求使得 $f(x) > f(2x - 1)$ 成立的 $x$ 的取值范围.
因为 $f(x) = f(-x) = x^2 - \dfrac{1}{x^2 + 1}$,
所以 $f(x)$ 是偶函数.
观察在 $x \in (0, +\infty)$ 上的单调性:
$x \nearrow$,$x^2 \nearrow$,$\dfrac{1}{x^2 + 1} \searrow$,$-\dfrac{1}{x^2 + 1} \nearrow$,$x^2 - \dfrac{1}{x^2 + 1} \nearrow$.
所以在 $y$ 轴左侧,$f(x) \searrow$,在 $y$ 轴右侧,$f(x) \nearrow$.
画出近似图象.
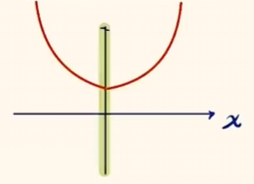
则当 $f(x) > f(2x - 1)$ 成立时,$|x| > |2x - 1|$.
则 $x^2 > (2x - 1)^2$.
即 $3x^2 - 4x + 1 < 0$.
所以 $x \in (\dfrac{1}{3}, 1)$.
示例2: 定义在 $\mathbb{R}$ 上的奇函数 $f(x)$ 满足 $f(2) = 3$,且函数 $g(x) = f(x) - 2x$ 在 $[0, +\infty)$ 上单调递减,求不等式 $f(x - 1) > 2x - 1$ 的解集.
注意到 $g(-x) = f(-x) - 2(-x) = -f(x) + 2x = -g(x)$.
所以 $g(x)$ 是奇函数.
所以 $g(-2) = -g(2) = -f(2) + 2 \times 2 = 1$.
因为 $g(x - 1) = f(x - 1) - 2x + 2$,
所以 $g(x - 1) + 2x - 2 > 2x - 1$.
化简得 $g(x - 1) > 1$.
即 $g(x - 1) > g(-2)$.
因为 $g(x)$ 在 $\mathbb{R}$ 上单调递减,
所以 $x - 1 < -2$.
所以 $x \in (-\infty, -1)$.
对称性
对称性的表达式推导
- 普通轴对称:
$f(a + x) = f(b - x) \implies$ 对称轴为直线 $x = \dfrac{a + b}{2}$.
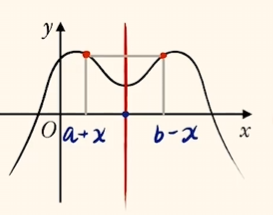
- 普通中心对称:
$f(a + x) + f(b - x) = c \implies$ 对称中心为点 $(\dfrac{a + b}{2}, \dfrac{c}{2})$.
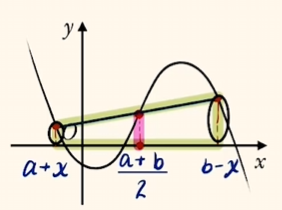
证明: 记对称中心为点 $C$,则 $x_C = \dfrac{a + b}{2}$,因为点 $C$ 到 $x$ 轴的距离是梯形的中位线,所以 $y_C = \dfrac{f(a + x) + f(b - x)}{2} = \dfrac{c}{2}$,所以点 $C(\dfrac{a + b}{2}, \dfrac{c}{2})$.
区别于周期性: $x$ 应异号.
例题
示例1: 若 $f(1 - x) = -f(3 + x)$ 恒成立,则函数 $f(x + 2)$ 的图象关于什么对称?
据题意,$f(1 - x) + f(3 + x) = 0$.
则函数 $f(x)$ 关于点 $(2, 0)$ 中心对称.
因为函数 $f(x + 2)$ 可由 $f(x)$ 向左平移 $2$ 个单位长度得到,
所以函数 $f(x + 2)$ 关于原点 $(0, 0)$ 中心对称.
示例2: 已知 $\forall x \in \mathbb{R},\; f(x) + f(4 - x) = 0$,若函数 $f(x)$ 与 $y = \dfrac{1}{x - 2}$ 图象交点横坐标分别为 $x_1,\; x_2,\; x_3,\; \ldots,\; x_n$,求 $x_1 + x_2 + x_3 + \ldots + x_n$.
据题意,函数 $f(x)$ 关于点 $(2, 0)$ 中心对称.
注意到 $y = \dfrac{1}{x - 2}$ 关于直线 $x = 2$ 对称.
所以图象交点 $(x_1, f(x_1)),\; (x_2, f(x_2)),\; (x_3, f(x_3)),\; \ldots ,\; (x_n, f(x_n)),\;$ 关于点 $(2, 0)$ 中心对称.
对于任意关于点 $C(p, q)$ 中心对称的点 $A(a, f(a))$ 与点 $B(b, f(b))$,有 $\dfrac{a + b}{2} = p$,$\dfrac{f(a) + f(b)}{2} = q$,
所以 $a + b = 2p$,$f(a) + f(b) = 2q$.
则如果点 $(x_1, f(x_1)),\; (x_2, f(x_2)),\; (x_3, f(x_3)),\; \ldots ,\; (x_n, f(x_n)),\;$ 关于点 $C(p, q)$ 中心对称,则 $x_1 + x_2 + x_3 + \ldots + x_n = np$,$f(x_1) + f(x_2) + f(x_3) + \ldots + f(x_n) = nq$.
因为图象交点 $(x_1, f(x_1)),\; (x_2, f(x_2)),\; (x_3, f(x_3)),\; \ldots ,\; (x_n, f(x_n)),\;$ 关于点 $(2, 0)$ 中心对称,
所以 $x_1 + x_2 + x_3 + \ldots + x_n = 2n$.
周期性
- 若 $f(x + a) = f(x)$,则函数 $f(x)$ 的周期 $T = a$.
- 若 $f(x + a) = -f(x)$,则函数 $f(x)$ 的周期 $T = 2a$.
证明: 因为 $f(x + a) = -f(x)$,所以 $f(x + 2a) = -f(x + a) = f(x)$,所以周期 $T = 2a$. - 若 $f(x + a) = \dfrac{k}{f(x)} \; (k \neq 0)$,则函数 $f(x)$ 的周期 $T = 2a$.
证明: 因为 $f(x + a) = \dfrac{k}{f(x)}$,所以 $f(x + 2a) = \dfrac{k}{f(x + a)} = \dfrac{k}{\dfrac{k}{f(x)}} = f(x)$,所以周期 $T = 2a$.
区别于对称性: $x$ 应同号.
示例1: $f(x + 1) = f(x) - f(x - 1)$ 是什么意思?
$f(x + 2) = f(x + 1) - f(x)$
$f(x + 2) = f(x) - f(x - 1) - f(x)$
$f(x + 2) = -f(x - 1)$
$f(x + 3) = -f(x)$
$f(x + 6) = -f(x + 3)$
$f(x + 6) = f(x)$
则周期 $T = 6$.
示例2: 已知定义在 $\mathbb{R}$ 上的函数 $f(x)$ 满足 $f(x + 3) = -f(x)$,且 $f(-1) = 2$,求 $f(2024)$.
据题意,周期 $T = 6$.
则 $f(2024) = f(2)$.
当 $x = -1$ 时, $f(2) = -f(-1)$,
所以 $f(2024) = f(2) = -f(-1) = -2$.
示例3: 已知函数 $f(x)$ 的定义域为 $\mathbb{R}$,且 $f(x + y) + f(x - y) = f(x)f(y)$,$f(1) = 1$,求 $f(1) + f(2) + \cdots + f(22)$.
令 $y = 1$,则 $f(x + 1) + f(x - 1) = f(x)$.
则函数周期 $T = 6$.
则原式 $= 3 \cdot [f(1) + f(2) + \cdots + f(6)] + f(1) + f(2) + f(3) + f(4)$.
令 $x = y = 0$,则 $2f(0) = f^2(0)$,所以 $f(0) = 0$ 或 $2$.
令 $y = 0$,则 $2f(x) = f(x)f(0)$.
故 $f(0) = 2$.
令 $x = y = 1$,则 $f(2) + 2 = 1$,所以 $f(2) = -1$.
在 $f(x + 1) + f(x - 1) = f(x)$ 中,
令 $x = 2$,则 $f(3) + 1 = -1$,所以 $f(3) = -2$.
依此类推,$f(4) = -1$,$f(5) = 1$,$f(6) = 2$.
原式 $= 3 \times 0 + 1 - 1 - 2 - 1 = -3$.
幂函数
分数指数幂
$$x^{\frac{1}{m}} = \sqrt[m]{x} \quad (x \geq 0)$$ $$x^{\frac{n}{m}} = \sqrt[m]{x^n} \quad (x \geq 0)$$证明1:
$\because x = x$,
$\therefore (x^{\frac{1}{m}})^m = (\sqrt[m]{x})^m$.
$\therefore x^{\frac{1}{m}} = \sqrt[m]{x}$
证明2:
$\because x^{\frac{1}{m}} = \sqrt[m]{x}$,
$\therefore x^{\frac{n}{m}} = x^{n \cdot \frac{1}{m}} = (x^n)^\frac{1}{m} = \sqrt[m]{x^n}$.
注意: 对于 $a \in \mathbb{R}$,有
$$a^{\frac{n}{n}} = \left\{ \begin{array}{lr} a,\; a \in \{a\,|\,a = 2k + 1, k \in \mathbb{Z}\}\\ |a|,\; a \in \{a\,|\,a = 2k, k \in \mathbb{Z}\} \end{array} \right. $$
幂函数
幂函数: 形如 $f(x) = x^a$ 的函数.
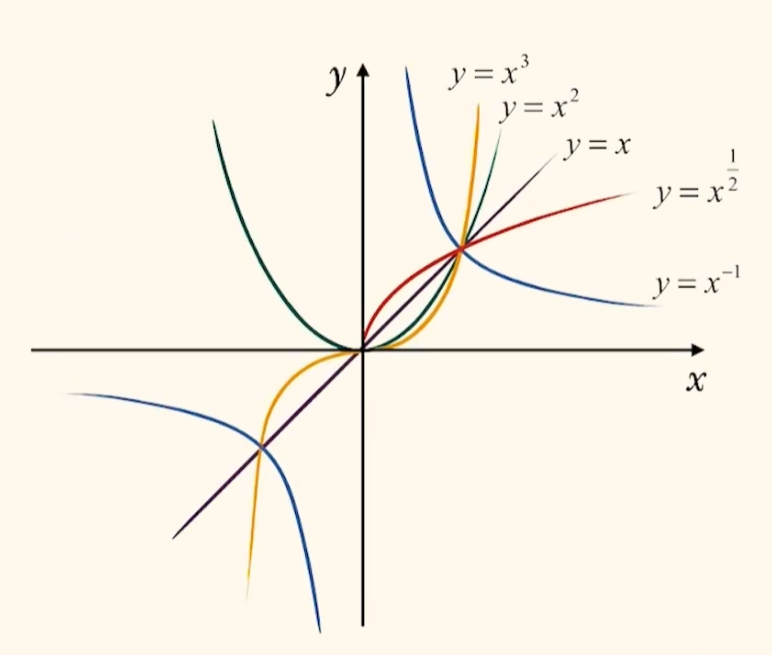
显然对于 $f(x) = x^a$,图象总过点 $(0, 0)$.
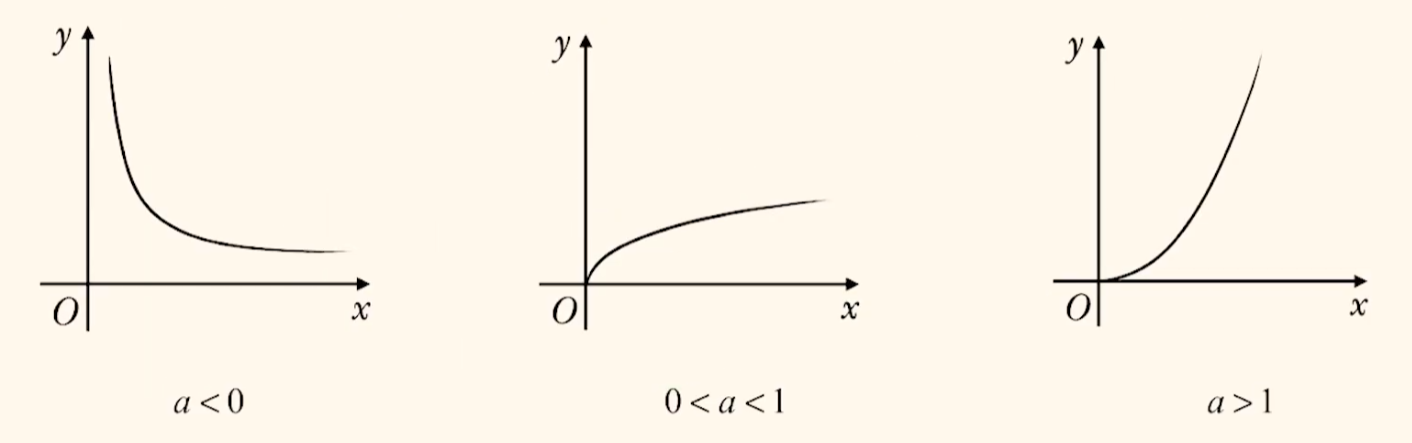
在第一象限内,$a < 0$ 时,函数单调递减;当 $0 < a < 1$ 时,函数单调递增;当 $a > 1$ 时,函数迅速单调递增.
当 $a < 0$ 时,在 $(1, +\infty)$ 上,$a$ 越小,横坐标相同时,纵坐标离 $x$ 轴越近.
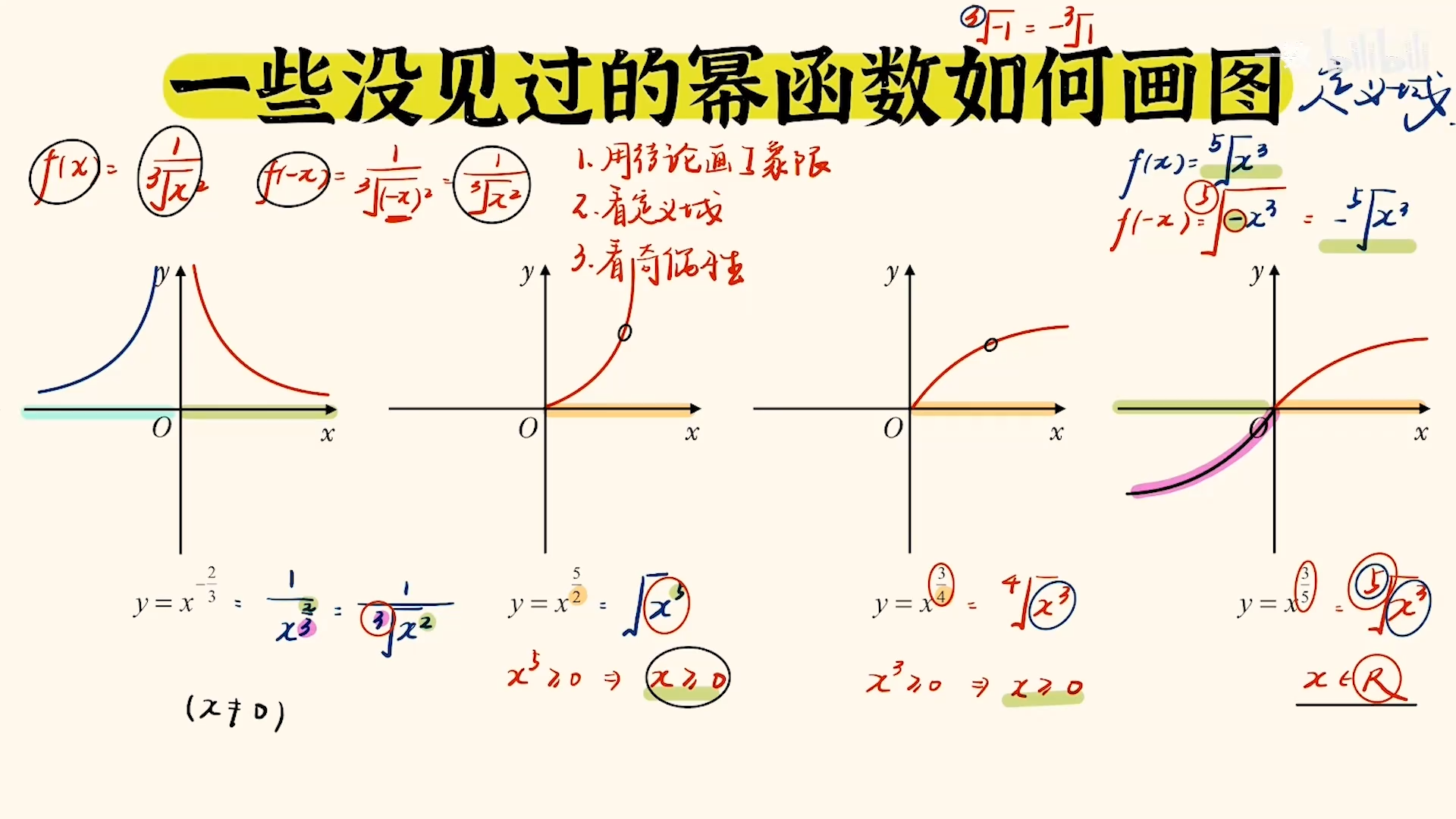
画幂函数:
- 用结论画第一象限.
- 看定义域.
- 看奇偶性.
注意: 幂函数中系数一定为 $1$.
示例: 已知幂函数 $f(x) = (m^2 - m - 1)x^m$ 的图象是关于 $y$ 轴对称的图形,求实数 $m$.
据题意 $m^2 - m - 1 = 1$.
解得 $m_1 = 2$,$m_2 = -1$.
因为 $f(x)$ 的图象是关于 $y$ 轴对称的图形,
所以 $m = 2$.
指数函数
指数函数: 形如 $f(x) = a^x$ 的函数.($a > 0$ 且 $a \neq 1$)
- 定义域: $\mathbb{R}$.
- 值域: $(0, +\infty)$.
- 单调性: $a > 1$ 时单调递增,$0 < a < 1$ 时单调递减.
- 渐近线: $x$ 轴.
- 定点: 点 $(0, 1)$.
- 对称性: $y = a^x$ 与 $y = (\dfrac{1}{a})^x$ 关于 $y$ 轴对称.
对数函数
对数
指对互化
$$x = \log_a b \iff a^x = b$$$a$ 叫做底数,$b$ 叫做真数.
注意: $a > 0$ 且 $a \neq 1$,$b > 0$.
推论1: $\log_a 1 = 0$,$\log_a a = 1$.
推论2: $a^{\log_a b} = b$,$x = \log_a a^x$.
数乘运算
$$\log_{x^m} y^n = \dfrac{n}{m}\log_x y$$导数
概念
$x_0$ 处的导数: $f'(x_0) = \lim\limits_{\Delta x \to 0} \dfrac{f(x_0 + \Delta x) - f(x_0)}{\Delta x}$
$\implies f(x)$ 的导函数: $f'(x) = \lim\limits_{\Delta x \to 0} \dfrac{f(x + \Delta x) - f(x)}{\Delta x}$
常见导数
- 常数: $c' = 0$.
- 幂函数: $(x^a)' = ax^{a - 1}$,推广(复合求导法则): $(m^a)' = am^{a - 1} \cdot m'$($m$ 是整式).
- 三角函数: $(\sin x)' = \cos x$,$\cos x = -\sin x$.
- 指数函数: $(a^x)' = a^x \ln a$,特别地,$(e^x)' = e^x$.
- 对数函数: $(\log_a x)' = \dfrac{1}{x \ln a}$,特别地,$(\ln x)' = \dfrac{1}{x}$.
复合求导法则: $f'(g(x)) = f'(x) \cdot g'(x)$.
常用实例: $(\dfrac{1}{x})' = -\dfrac{1}{x^2}$,$(\sqrt{x})' = \dfrac{1}{2\sqrt{x}}$.
待补课程
- 抽象函数性质综合
- 抽象函数 + 恒成立 + 构造函数
