概念
任意角
角: 由始边到终边旋转的度数,角度 $\theta \in \mathbb{R}$.
由始边逆时针转的角: 正角.
由始边顺时针转的角: 负角.
逆时针转角变大,顺时针转角变小.
示例1: 时钟经过 $4 \,\mathrm{h}$,转过了 $-120^\circ$.
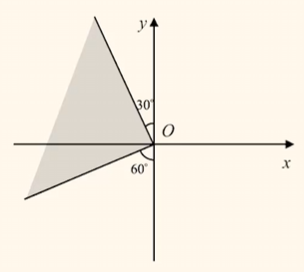
示例2: 如图,已知角 $\theta$ 终边在图中阴影所表示的范围内(不含边界),那么$\theta \in \{\theta \,|\, 120^\circ + k \cdot 360^\circ < \theta < 210^\circ + k \cdot 360^\circ, k \in \mathbb{Z}\}$.
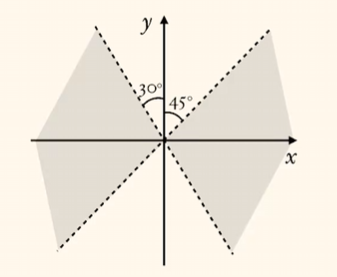
示例3: 如图,已知角 $\alpha$ 终边在图中阴影所表示的范围内(不含边界),那么$\alpha \in \{\alpha \;| -60^\circ + k \cdot 180^\circ < \alpha < 45^\circ + k \cdot 180^\circ, k \in \mathbb{Z}\}$.
象限角
如角的终边在第 $X$ 象限,则该角为第 $X$ 象限角.
弧度制
在弧长为 $l$,半径为 $r$ 的扇形中,角度 $\theta = \dfrac{l}{r}$,单位为 $\mathrm{rad}$,通常省略不写.
则 $180^\circ = \pi$.
$x\pi \,\mathrm{rad} = x \cdot 180^\circ$.
$x^\circ = x \cdot \dfrac{\pi}{180}\,\mathrm{rad}$.
常见角度与弧度:
| $0^\circ{}$ | $30^\circ$ | $45^\circ$ | $60^\circ$ | $90^\circ$ | $120^\circ$ | $135^\circ$ | $150^\circ$ | $180^\circ$ |
|---|---|---|---|---|---|---|---|---|
| $0$ | $\dfrac{\pi}{6}$ | $\dfrac{\pi}{4}$ | $\dfrac{\pi}{3}$ | $\dfrac{\pi}{2}$ | $\dfrac{2\pi}{3}$ | $\dfrac{3\pi}{4}$ | $\dfrac{5\pi}{6}$ | $\pi$ |
在弧长为 $l$,半径为 $r$ 的扇形中,角度为 $\theta$,因为 $\theta = \dfrac{l}{r}$,所以弧长 $l = \theta r$,面积 $S = \dfrac{\theta r^2}{2} = \dfrac{lr}{2}$.
三角函数
如图,在单位圆 $x^2 + y^2 = 1$ 中,点 $(x_0, y_0)$ 在圆上,记角为 $\theta$,则三角函数分别为
三角函数的正负规律:
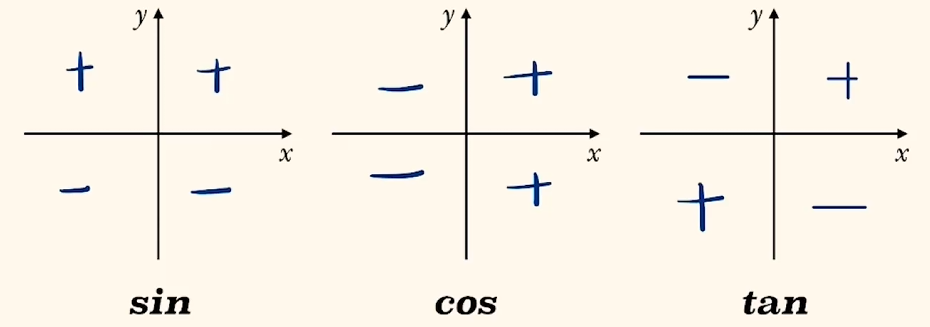
记忆口诀: ASTC.(从第一象限依次到第四象限,为正的分别是All,$\sin$,$\tan$,$\cos$)
同角三角函数关系
$$\tan \theta = \dfrac{\sin \theta}{\cos \theta}$$ $$\sin^2 \theta + \cos^2 \theta = 1$$知一求二
示例:
已知 $\alpha$ 是第二象限角,若 $\sin \alpha = \dfrac{2}{3}$,求 $\cos \alpha$,$\tan \alpha$.
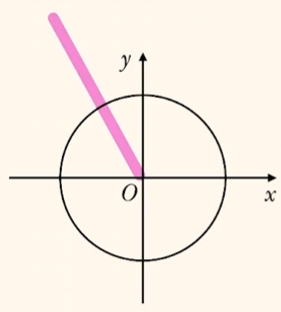
方法一: 解方程.
由 $\sin^2 \alpha + \cos^2 \alpha = 1$ 得,$\cos^2 \alpha = \dfrac{5}{9}$,所以 $\cos \alpha = \pm \dfrac{\sqrt{5}}{3}$.
因为 $\alpha$ 是第二象限角,所以 $\cos \alpha < 0$,则 $\cos \alpha = -\dfrac{\sqrt{5}}{3}$.
所以 $\tan \alpha = \dfrac{\dfrac{2}{3}}{-\dfrac{\sqrt{5}}{3}} = -\dfrac{2\sqrt{5}}{5}$.
方法二: 当 $\alpha$ 为锐角时,画辅助三角形.
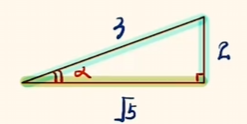
由图可得 $\cos \alpha = \dfrac{\sqrt{5}}{3}$,$\tan \alpha = \dfrac{2\sqrt{5}}{5}$.
因为 $\alpha$ 是第二象限角,所以 $\cos \alpha < 0$,则 $\cos \alpha = -\dfrac{\sqrt{5}}{3}$,$\tan \alpha = -\dfrac{2\sqrt{5}}{5}$.
凑齐次式
示例1: 已知 $\tan \theta = 2$,求 $\sin^2 \theta + \sin \theta \cos \theta - 2 \cos^2 \theta$.
$
\begin{aligned}
& \quad\; \sin^2 \theta + \sin \theta \cos \theta - 2 \cos^2 \theta \\
&= \dfrac{\sin^2 \theta + \sin \theta \cos \theta - 2 \cos^2 \theta}{\sin^2 \theta + \cos^2 \theta} \\
&= \dfrac{\dfrac{\sin^2 \theta + \sin \theta \cos \theta - 2 \cos^2 \theta}{\cos^2 \theta}}{\dfrac{\sin^2 \theta + \cos^2 \theta}{\cos^2 \theta}} \\
&= \dfrac{\tan^2 \theta + \tan \theta - 2}{\tan^2 \theta + 1} \\
&= \dfrac{4 + 2 - 2}{4 + 1} \\
&= \dfrac{4}{5}
\end{aligned}
$
示例2: 已知 $\tan \theta = 2$,求 $1 + \sin \theta \cos \theta$ 的值.
$
\begin{aligned}
& \quad\; 1 + \sin \theta \cos \theta \\
&= \sin^2 \theta + \cos^2 \theta + \sin \theta \cos \theta \\
&= \dfrac{\sin^2 \theta + \cos^2 \theta + \sin \theta \cos \theta}{\sin^2 \theta + \cos^2 \theta} \\
&= \dfrac{\dfrac{\sin^2 \theta + \cos^2 \theta + \sin \theta \cos \theta}{\cos^2 \theta}}{\dfrac{\sin^2 \theta + \cos^2 \theta}{\cos^2 \theta}} \\
&= \dfrac{\tan^2 \theta + 1 + \tan \theta}{\tan^2 \theta + 1} \\
&= \dfrac{4 + 1 + 2}{4 + 1} \\
&= \dfrac{7}{5}
\end{aligned}
$
诱导公式
$$\sin (-\theta) = -\sin \theta$$ $$\cos (-\theta) = \cos \theta$$ $$\tan (-\theta) = -\tan \theta$$$$\sin (\dfrac{k\pi}{2} \pm \theta) = \left\{ \begin{array}{lr} \pm \cos \theta,\; k \in \{k \,|\, k = 2n + 1, n \in \mathbb{Z}\} \\ \pm \sin \theta,\; k \in \{k \,|\, k = 2n, n \in \mathbb{Z}\} \end{array} \right. $$
$$\cos (\dfrac{k\pi}{2} \pm \theta) = \left\{ \begin{array}{lr} \pm \sin \theta,\; k \in \{k \,|\, k = 2n + 1, n \in \mathbb{Z}\} \\ \pm \cos \theta,\; k \in \{k \,|\, k = 2n, n \in \mathbb{Z}\} \end{array} \right. $$
$$\tan (\dfrac{k\pi}{2} \pm \theta) = \left\{ \begin{array}{lr} \pm \cot \theta,\; k \in \{k \,|\, k = 2n + 1, n \in \mathbb{Z}\} \\ \pm \tan \theta,\; k \in \{k \,|\, k = 2n, n \in \mathbb{Z}\} \end{array} \right. $$
假设 $\theta \in [0, \dfrac{\pi}{2}]$,观察前后的正负,并根据情况添加符号.
即在自变量的 $\dfrac{k\pi}{2} \pm \theta$ 中,整数 $k$
示例: 已知 $\cos^2 \theta - 2\sin \theta \sin (\theta + \dfrac{\pi}{2}) = 4\sin \theta + 2\sin (\dfrac{3\pi}{2} - \theta)$,求 $\dfrac{2 + \sin \theta \sin (\dfrac{\pi}{2} + \theta)}{1 - \tan (\theta - \pi)}$ 的值.
由诱导公式得 $\sin (\theta + \dfrac{\pi}{2}) = \cos \theta$,$\sin (\dfrac{3\pi}{2} - \theta) = -\cos \theta$,$\tan (\theta - \pi) = \tan \theta$.
则原等式变形为 $\cos^2 \theta - 2\sin \theta \cos \theta = 4\sin \theta - 2\cos \theta$.
提公因式得 $\cos \theta (\cos \theta - 2\sin \theta) = -2(\cos \theta - 2\sin \theta)$.
则 $(\cos \theta + 2)(\cos \theta - 2\sin \theta) = 0$.
因为 $\cos \theta \in [-1, 1]$,
所以 $\cos \theta \neq -2$.
所以 $\cos \theta - 2\sin \theta = 0$.
则 $\cos \theta = 2\sin \theta$.
所以 $\tan \theta = \dfrac{1}{2}$.
$
\begin{aligned}
& \quad\, \dfrac{2 + \sin \theta \sin (\dfrac{\pi}{2} + \theta)}{1 - \tan (\theta - \pi)} \\
&= \dfrac{2 + \sin \theta \cos \theta}{1 - \tan \theta} \\
&= \dfrac{2 + \sin \theta \cos \theta}{1 - \dfrac{1}{2}} \\
&= 4 + 2\sin \theta \cos \theta \\
&= 4 + \dfrac{2\sin \theta \cos \theta}{\sin^2 \theta + \cos^2 \theta} \\
&= 4 + \dfrac{\dfrac{2\sin \theta \cos \theta}{\cos^2 \theta}}{\dfrac{\sin^2 \theta + \cos^2 \theta}{\cos^2 \theta}} \\
&= 4 + \dfrac{2\tan \theta}{\tan^2 \theta + 1} \\
&= 4 + \dfrac{1}{\dfrac{1}{4} + 1} \\
&= \dfrac{24}{5}
\end{aligned}
$
两角和差公式
$$\cos (\alpha \pm \beta) = \cos \alpha \cos \beta \mp \sin \alpha \sin \beta$$ $$\sin (\alpha \pm \beta) = \sin \alpha \cos \beta \pm \cos \alpha \sin \beta$$ $$\tan (\alpha \pm \beta) = \dfrac{\tan \alpha \pm \tan \beta}{1 \mp \tan \alpha \tan \beta}$$可知常见角三角函数值
| $\theta$ | $0^\circ$ | $15^\circ$ | $30^\circ$ | $45^\circ$ | $60^\circ$ | $75^\circ$ | $90^\circ$ |
|---|---|---|---|---|---|---|---|
| $\sin \theta$ | $0$ | $\dfrac{\sqrt{6} - \sqrt{2}}{4}$ | $\dfrac{1}{2}$ | $\dfrac{\sqrt{2}}{2}$ | $\dfrac{\sqrt{3}}{2}$ | $\dfrac{\sqrt{6} + \sqrt{2}}{4}$ | $1$ |
| $\cos \theta$ | $1$ | $\dfrac{\sqrt{6} + \sqrt{2}}{4}$ | $\dfrac{\sqrt{3}}{2}$ | $\dfrac{\sqrt{2}}{2}$ | $\dfrac{1}{2}$ | $\dfrac{\sqrt{6} - \sqrt{2}}{4}$ | $0$ |
| $\tan \theta$ | $0$ | $2 - \sqrt{3}$ | $\dfrac{\sqrt{3}}{3}$ | $1$ | $\sqrt{3}$ | $2 + \sqrt{3}$ | 未定义 |
公式推导:
方法一 画图,其中 $\alpha$,$\beta \in (0, \dfrac{\pi}{2})$
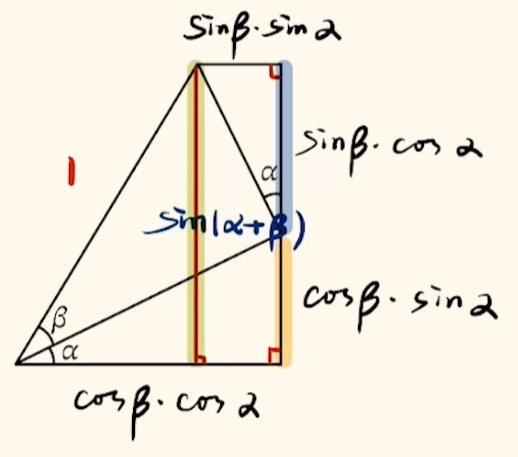
得出
$$\cos (\alpha + \beta) = \cos \alpha \cos \beta - \sin \alpha \sin \beta$$
$$\sin (\alpha + \beta) = \sin \alpha \cos \beta + \cos \alpha \sin \beta $$
由三角函数的奇偶性与 $\tan \theta = \dfrac{\sin \theta}{\cos \theta}$ 整理可得
$$\cos (\alpha \pm \beta) = \cos \alpha \cos \beta \mp \sin \alpha \sin \beta $$
$$\sin (\alpha \pm \beta) = \sin \alpha \cos \beta \pm \cos \alpha \sin \beta $$
$$\tan (\alpha \pm \beta) = \dfrac{\tan \alpha \pm \tan \beta}{1 \mp \tan \alpha \tan \beta} $$
方法二 利用单位圆,其中 $\alpha$,$\beta \in \mathbb{R}$
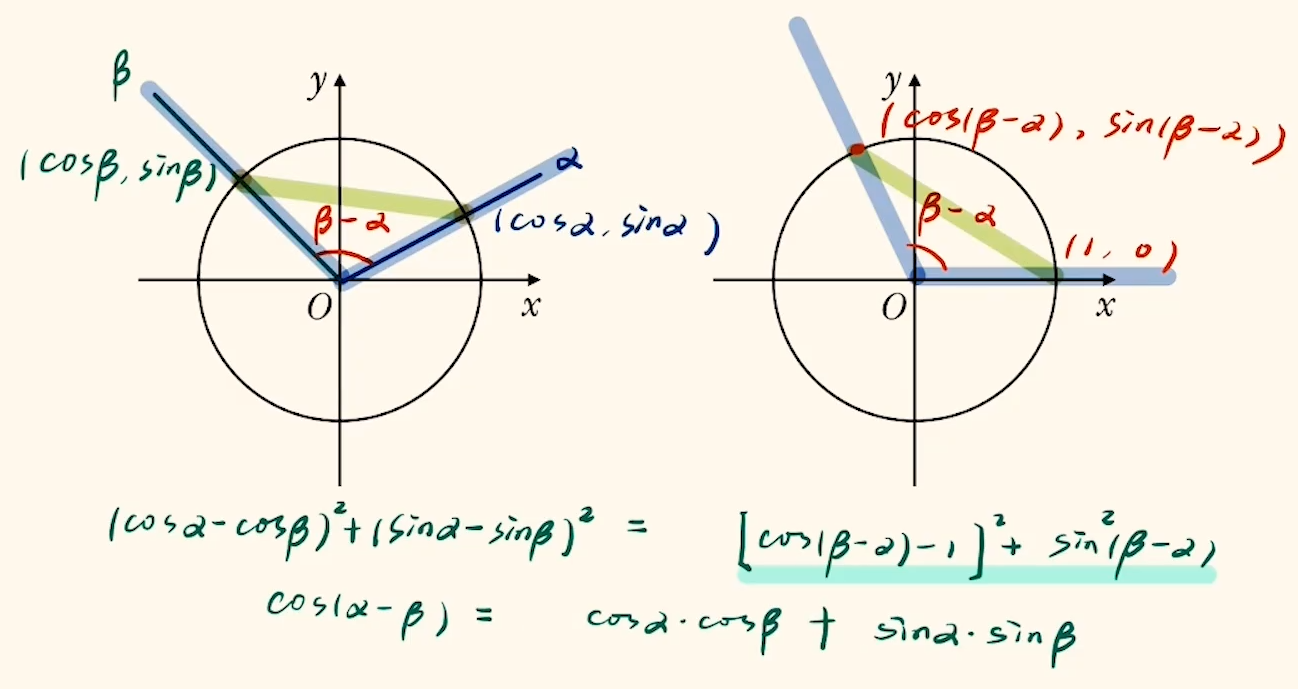
得出
$$\cos (\alpha - \beta) = \cos \alpha \cos \beta + \sin \alpha \sin \beta $$
$$\sin (\alpha - \beta) = \sin \alpha \cos \beta - \cos \alpha \sin \beta $$
由三角函数的奇偶性与 $\tan \theta = \dfrac{\sin \theta}{\cos \theta}$ 整理可得
$$\cos (\alpha \pm \beta) = \cos \alpha \cos \beta \mp \sin \alpha \sin \beta $$
$$\sin (\alpha \pm \beta) = \sin \alpha \cos \beta \pm \cos \alpha \sin \beta $$
$$\tan (\alpha \pm \beta) = \dfrac{\tan \alpha \pm \tan \beta}{1 \mp \tan \alpha \tan \beta} $$
辅助角公式
$$A \sin \alpha + B \cos \alpha = \sqrt{A^2 + B^2} \sin (\alpha + \phi)$$推论:
当 $\alpha \in \mathbb{R}$ 时,有 $\sin (\alpha + \phi) \in [-1, 1]$,则 $-\sqrt{A^2 + B^2} \leq \sqrt{A^2 + B^2} \sin (\alpha + \phi) \leq \sqrt{A^2 + B^2}$,所以

