信息技术

语言入门

ASCII码表重要字符

1
2
3
'0'=48
'A'=65
'a'=97

变量类型转换

1
2
3
4
5
float a;
int b, c;
cin >> a;
b = (int)a;
c = int(a);

这里的b和c本质是一样的，都将float类型的a转换成了int类型的.
如果是int类型转浮点类型，还可以使用如a = 1.0 * b的方法.

C的输入输出占位符

占位符 说明
%d 十进制整数，一般用于int
%nd 输出整数，前面用空格补齐直到够n位
%I64d（Windows）
%lld（Linux）		 十进制整数，一般用于long long
%f 读入float类型，输出float或double类型，默认保留6位小数
%lf 读入double类型
%.nf 输出保留n位小数的浮点数
%0nd 输出整数，前面用0补齐直到够n位
%c char类型的字符
%s string类型的字符串，读入时不应加取地址运算符&

switch-case语句

1
2
3
4
5
6
7
8
9
10
char c;
cin >> c;
switch (c) {
    case 'a': cout << 1 << ' ';
    case 'b': cout << 2 << ' '; break;
    case 'c': case 'd':
        cout << 3 << ' ';
        break;
    default: cout << 0 << ' ';
}

当c为'a'时，会输出1 2 ，为'b'时会输出2 ，为'c'或'd'时会输出3 ，不是上面任意一种情况时会输出0 .

随机数

1
2
3
4
int a;
srand(time(0));
a = rand() % 100 + 1;
cout << a;

这里的srand()函数设定了随机数种子为当前时间，time(0)为获取当前时间，需使用<ctime>头文件，rand()函数根据随机数种子获取伪随机数，最终a的取值范围为 $[1, 100]$.

自增语句

1
2
3
int i = 1, a[10] = {0};
a[i++] = 1;
a[++i] = 2;

该代码块等效于

1
2
3
4
5
int i = 1, a[10] = {0};
a[i] = 1;
i++;
++i;
a[i] = 2;

故最终a[1]的值为1，a[3]的值为2，其余为0.

浮点数精度误差处理

1
2
3
4
5
int n = 10;
for (double i = 0.1; i != n; i += 0.1) {
    ...
}
cout << "broken";

发现程序死循环，无输出，即存在浮点数精度误差导致10 != 10，可以将循环修改成如下条件

1
2
3
for (double i = 0.1; n - i <= 1e-2; i += 0.1) {
    ...
}

其中1e-2是可接受的精度误差，也可视情况写成1e-3等.

枚举法判断质数

如果一个数 $x$ 存在不是 $1$ 或自身的因数，那么会成对出现，即 $ab = x$，且如果 $a < \sqrt{x}$ 则 $b > \sqrt{x}$，显然只要枚举 $[2, \sqrt{x}] \cap \mathbb{Z}$ 间的数即可，代码实现如下

1
2
3
4
5
6
7
8
9
bool is_prime(int x) {
    if (x == 0 || x == 1) {return false;}
    for (int i = 2; i * i <= x; i++) {
        if (x % i == 0) {
            return false;
        }
    }
    return true;
}

do-while语句

1
2
3
do {
    ...
} while (x);

等效于

1
2
3
while (x) {
    ...
}

memset()函数

1
2
int a[100];
memset(a, 0, sizeof(a));

该函数需要<cstring>头文件，第二个参数为0时，数组初始化为0；为-1或255时，初始化为-1；为127时，初始化为趋近于INT_MAX的正数；为128时，初始化为趋近于-INT_MAX的负数.

字符相关函数

  1. 字符数组相关
1
2
3
4
5
6
7
8
9
char s, c[100] = "Hello"; // 初始化字符数组可以直接赋值
strcpy(s, c); //将字符数组 c 拷贝到 s 中
int l = strlen(c); // 查询字符数组的长度

char d[100] = "Luogu";
if (strcmp(c, d) < 0) {cout << "c < d";}
if (strcmp(c, d) = 0) {cout << "c = d";}
if (strcmp(c, d) > 0) {cout << "c > d";}
// 按照字典序比较字符数组大小
1
2
3
4
5
6
7
8
9
10
11
12
char c, s[100], t[100], u[100];
c = getchar(); // 返回读取的单个字符
putchar(c); // 输出单个字符

fgets(s, sizeof(s), stdin); // 输入整行字符串
puts(s); // 直接输出字符串

fgets(t, sizeof(t), stdin);
int a, b;
sscanf(t, "%d", &a); // 将字符串中的数读入至变量
cin >> b;
sprintf(u, "%d", b); // 将变量打印至字符串中
  1. 字符串相关
1
2
3
4
5
6
7
8
9
10
11
12
13
string s, t;
getline(cin, s); // 输入整行字符串
cin >> t;
s += t; // 等价于 s.append(t);
int l = s.length(); // s.length() 也可写作 s.size()
if (s < t) {cout << "s < t";}

int pos, len;
cin >> pos >> len;
s = s.substr(pos, len); // 在 pos 处截长度为 len 的字符串
s = s.insert(pos, t); // 在 pos 处插入字符串 t
cout << (int)s.find(t, pos); // 从 pos 处开始寻找字符串 t，找不到则返回 -1，pos 可以省略
// 注意 pos 为字符串下标，应从 0 开始计算

注意使用cin读入一个独占数字后，读入指针会在这一行的末尾，再使用getline()读入字符串时，只会读到空串（第一行），所以如果要读第二行，则需要假装读入空串，可以使用getline()或getchar()等.

  1. 字符串与字符数组

string转char方法一

1
2
3
4
char c[10]; string s;
getline(cin, s);
int l = s.copy(c, 9); // 从 s 复制 9 个字符到 c 中，返回复制长度
c[l] = '\0';

string转char方法二

1
2
3
4
char c[10]; string s;
getline(cin, s);
strcpy(c, s.c_str());
// 或者指定复制字符数 strncpy(c, s.c_str(), 10);

char转string

1
2
3
char c[10]; string s;
fgets(c, sizeof(c), stdin);
s = c;

初涉算法

结构体内部函数

构造函数

1
2
3
4
5
6
7
8
9
10
struct node {
    int a, b, c;
    node(int _a, int _b, int _c) {
        this->a = _a;
        this->b = _b;
        this->c = _c;
    } // 方便定义时直接传参，无歧义时 this-> 可以省略
    node() {} // 无参初始化
};
node x, y(1, 2, 3);

成员函数

1
2
3
4
5
6
7
8
9
10
11
12
13
struct node {
    int a, b, c;
    node(int _a, int _b, int _c) {
        a = _a;
        b = _b;
        c = _c;
    }
    int sum() {
        return a + b + c;
    }
};
node x(1, 2, 3);
cout << x.sum(); // 输出结果是 6

重载

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
struct node {
    int a[100] = {0};
    int &operator[](int i) {
        return a[i];
        // 可以直接用 x[i] 代表 x.a[i]，编写更加自然
        // 注意重载类型与返回类型一致，下标重载定义时需取地址
    }
    node operator+(node b) {
        node c;
        c[1] = a[1] * 10 + b[1] * 10;
        return c;
    } // 重载 + 运算符
};
node x, y, z;
x[1] = 1, y[1] = 1;
z = x + y;
cout << z[1]; // 输出结果是 20

STL中sort()函数自定义排序规则

1
2
3
4
5
6
7
bool cmp(int a, int b) {
    return a > b; // 从大到小排序
}
int a[11], n; cin >> n;
for (int i = 1; i <= n; i++) {cin >> a[i];}
sort(a + 1, a + 1 + n, cmp); // 排序下标在[1, n + 1)上的数
for (int i = 1; i <= n; i++) {cout << a[i];}

子集枚举

考虑有限集合 $A = \{1, 2, 3, 4, 5\}$，可以通过二进制数1和0表示其元素的有无，则A对应二进制11111，则子集 $\{2, 5\}$ 可表示为01001，则易用位运算表示集合的运算.
当存在有限集合 $A$ 与 $B$ 时，它们的二进制数分别用它们的小写字母表示，则集合运算用位运算方式表示如下.

  1. 并集:
    若 $A \cup B = C$，则c = a | b.
  2. 交集:
    若 $A \cap B = C$，则c = a & b.
  3. 包含:
    若 $A \subseteq B \implies A \cup B = B$，$A \cap B = A$，则 (a | b == b) && (a & b == a)为真.
  4. 属于:
    若 $x \in A$，且 $x$ 为集合 $A$ 的第 n 个元素，则构造集合 $C = \{x\}$，易得 $C \subseteq A$，
    那么c = 1 << (n - 1)且c & a为真，则1 << (n - 1) & a为真.
  5. 补集
    已知全集 $U$，若 $B = \complement_U{A}$，则a与b的每一位都不一样，则b = u ^ a.

可以用内建函数__builtin_popcount()查询该数在二进制下1的个数.

1
2
int x = 5; // 101
cout << __builtin_popcount(x); // 输出为 2

next_permutation()函数

1
2
3
4
5
int a[3] = {1, 2, 3};
printf("%d %d %d\n", a[0], a[1], a[2]);
while(next_permutation(a, a + 3)) { // 排列下标在[1, n + 1)上的数
    printf("%d %d %d\n", a[0], a[1], a[2]);
}

需要包含<algorithm>头文件，函数直接对数组进行排列操作，如上代码输出为1 2 3一直到3 2 1的字典序全排列，当没有下一排列时返回0.

贪心算法

思想：每一步都选择当前状态下的最优解，从而达到全局最优.
需要证明其对于当前题目的正确性后才可使用.
方法一：使用反证法，假设选择的方案不是贪心方案，如果比找不出比贪心方案更优的方案，则贪心算法可用.
方法二：使用数学归纳法，每一步都是目前为止的最优解，一直到最后一步就是全局的最优解.

哈夫曼编码

思想：给出具有一定频数的项目，将频数最小的两项目合并，频数相加，作为一个项目参加接下来的合并，重复操作，则最终得到的总项目频数最小.
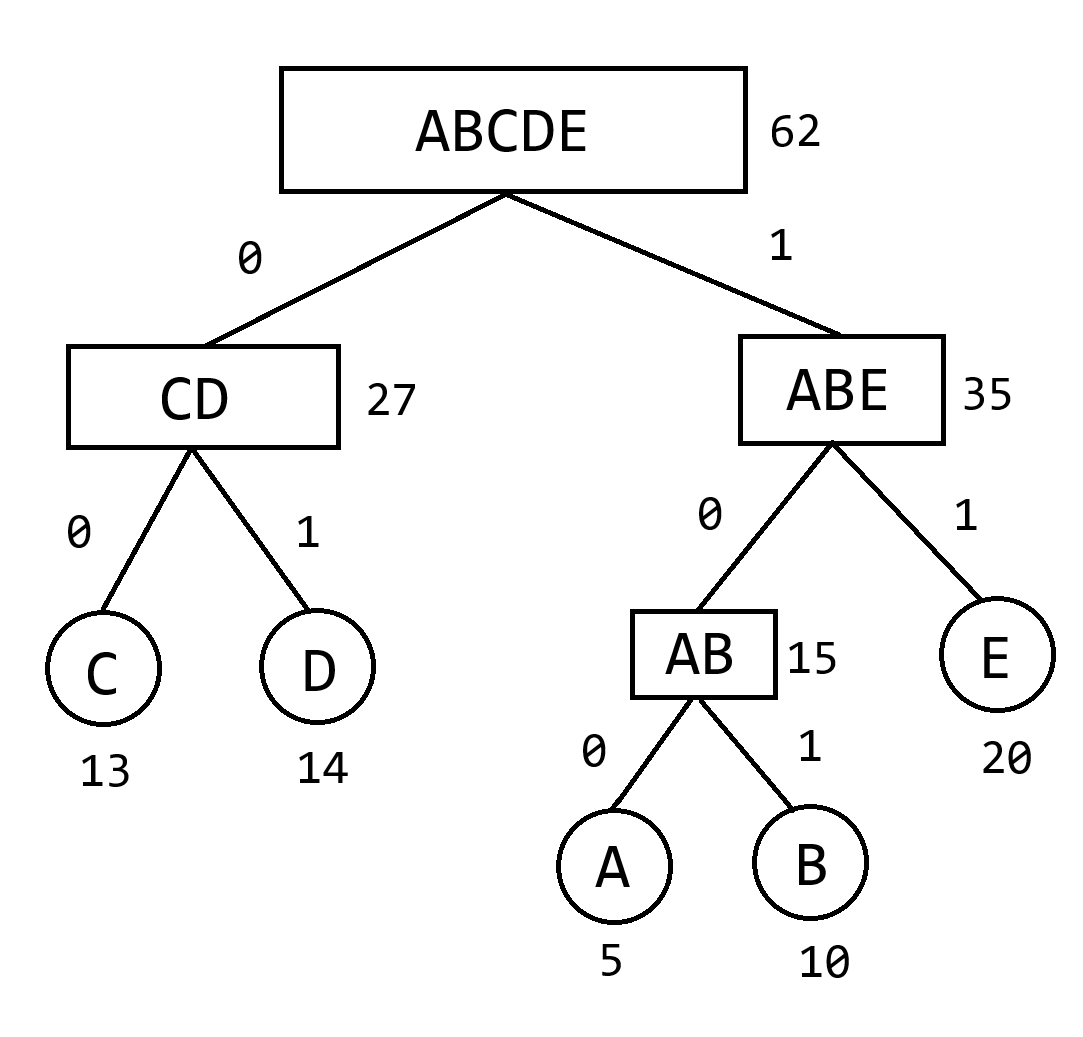
例：一段信息由A，B，C，D，E五个字母组成，其出现的次数分别是5，10，13，14，20，求最佳编码方案.
解：如图所示.

lower_bound()与upper_bound()

1
2
3
int a[5] = {1, 3, 3, 5, 5}
cout << lower_bound(a, a + 5, 3) - a << endl;
cout << upper_bound(a, a + 5, 3) - a << endl;

输出分别是1和3. 需要包含<algorithm>头文件，并对有序数组操作. 将第三个参数记为val，它们都是在左闭右开区间内寻找地址，lower_bound()可找到位置i使得a[i] >= val且a[i - 1] < val，upper_bound()可找到位置i使得a[i] > val且a[i - 1] <= val. 由于返回的是地址，因此得到下标需要减去数组名.
易得lower_bound(a, a + n, val + 1)等价于upper_bound(a, a + n, val).

简单数据结构

可变长度数组vector的用法

1
2
3
4
5
6
vector<int> v(100, -1); // 初始长度 100，每个元素初始化为 -1
v.push_back(1);
cout << v[100]; // 输出 1
int l = v.size(); // 101
v.resize(200, -2); // 长度变更为200，v[101] 到 v[199] 为 -2
v.resize(50); // 长度变更为 50，删去多余元素

需要头文件<vector>.

栈stack的用法

1
2
3
4
5
6
stack<int> s;
s.push(1);
cout << s.top() << endl; // 输出 1
s.pop();
cout << s.size() << endl; // 输出 0
if (s.empty()) {cout << "EMPTY";} // 输出 EMPTY

需要头文件<stack>.

队列queue的用法

1
2
3
4
5
6
7
queue<int> q;
q.push(1); q.push(2); q.push(3); // 分别将 1，2，3 压入队尾
q.pop();
cout << q.front() << endl; // 输出 2
cout << q.back() << endl; // 输出 3
cout << q.size(); // 输出 2
if (q.empty()) {cout << "EMPTY";} // 无输出

需要头文件<queue>;

链表list的用法与迭代器

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
int arr[5] = {1, 2, 3};
list<int> a(arr, arr + 3); // 将 arr 数组的前三个元素作为链表初始值
list<int>::iterator it; // 迭代器
cout << a.size() << endl; // 输出 3
it = a.begin(); // 指向开头的迭代器（闭）
cout << *it << endl; // 输出 1
it = a.end(); // 指向末尾的迭代器（开）
it--; // 指向上一元素，it++ 反之
cout << *it << endl; // 输出 3
a.push_front(0); // 链表开头插入 0
a.push_back(4); // 链表末尾插入 4
a.insert(++a.begin(), -1); // 在 1 前插入 -1，第一个参数应为迭代器
for (list<int>::iterator i = a.begin(); i != a.end(); i++) {cout << *i << " ";}
cout << endl; // 依次打印 0 -1 1 2 3 4
a.pop_front(); // 删除链表开头
a.pop_back(); // 删除链表末尾
a.erase(++a.begin()); // 删除 1，参数应为迭代器
for (list<int>::iterator i = a.begin(); i != a.end(); i++) {cout << *i << " ";}
// 依次打印 -1 2 3

需要头文件<list>.
通过元素的值快速定位元素位置可以定义如list<int>::iterator index[101]的索引来为每个值记录它的迭代器，方便查找它附近的元素.

基础数学与数论

逻辑命题

表示方法：

  1. 或：$A \lor B$，$A + B$.
  2. 与：$A \land B$，$A \cdot B$，$AB$.
  3. 非：$\lnot A$，$\overline{A}$.
  4. 异或：$A \oplus B$，等价于 $(A \land \lnot B) \lor (\lnot A \land B)$，$A\overline{B} + \overline{A}B$.

逻辑运算的性质：

  1. 交换律：$AB = BA$，$A + B = B + A$.
  2. 结合律：$(AB)C = A(BC)$，$(A + B) + C = A + (B + C)$.
  3. 分配律：$A(B + C) = AB + AC$.
  4. $A + 1 = 1$，$A + 0 = A$，$A \cdot 1 = A$，$A \cdot 0 = 0$.
  5. $A \cdot A = A$，$A + A = A$，$A + \overline{A} = 1$，$A \cdot \overline{A} = 0$.
  6. 德·摩根定律：$\overline{A} + \overline{B} = \overline{AB}$，$\overline{A} \cdot \overline{B} = \overline{A + B}$.

模运算的基本性质

  1. $(a + b + c) \bmod k = ((a + b) \bmod k + c) \bmod k$.
    证明：设 $a + b = kx + m$，
    则右边 $= (c + m) \bmod k$.
    而左边 $= (kx + c + m) \bmod k = (c + m) \bmod k$，
    $\therefore$ 左边 $=$ 右边.

  2. $(abc) \bmod k = ((ab) \bmod k \cdot c) \bmod k$.
    证明：设 $ab = kx + m$，
    则右边 $= cm \bmod k$.
    而左边 $= (ckx + cm) \bmod k = cm \bmod k$，
    $\therefore$ 左边 $=$ 右边.

排列组合

  1. 排列数
    当从 $n$ 个元素中抽取出 $m$ 个元素，排成一列的方案数用 $\mathrm{A}_n^m$ 表示，计算方法

    $$\mathrm{A}_n^m = \prod \limits_{i = 0}^{m - 1} (n - i) = \dfrac{n!}{(n - m)!} $$

  2. 组合数
    当从 $n$ 个元素中抽取出 $m$ 个元素，组合的方案数用 $\mathrm{C}_n^m$ 表示，计算方法

    $$\mathrm{C}_n^m = \dfrac{n!}{(n - m)! \cdot m!} $$

    证明：排列区分顺序，组合不区分顺序，故对于每一种组合，都有 $\mathrm{A}^m_m$ 种排列方式，则组合数 $\mathrm{C}^m_n = \dfrac{\mathrm{A}^m_n}{\mathrm{A}^m_m} = \dfrac{n!}{(n - m)! \cdot m!}$.